В.И. Арнольд "Задачи для детей от 5 до 15 лет"

Эти задачи я записал в Париже весной 2004 года, когда русские парижане попросили меня помочь их малолетним детям приобрести традиционную для России, но далеко превосходящую все западные обычаи культуру мышления.
Я глубоко убежден, что эта культура более всего воспитывается ранним самостоятельным размышлением о простых, но не легких вопросах, вроде приведенных ниже (рекомендую особенно задачи 1, 3, 13).
Мой долгий опыт показал, что отстающие в школе двоечники часто решают их лучше отличников, так как им на своей «камчатке» все время приходится для выживания думать больше, чем «чтоб управлять всей Севильей и Гренадой», как говорил о себе Фигаро, в то время как отличники не могут взять в толк, «что на что требуется умножать» в этих задачах.
Я заметил даже, что пятилетние дети решают подобные задачи лучше школьников, испорченных натаскиванием, которым они даются легче, чем студентам, подвергшимся зубрежке в университете, но все же превосходящим своих профессоров (хуже всех решают эти простые задачи нобелевские и филдсовские лауреаты)

1. У Маши не хватало для покупки букваря семи копеек, а у Миши одной копейки. Они сложились, чтобы купить один букварь на двоих, но денег все равно не хватило. Сколько стоил букварь?
2. Бутылка с пробкой стоит 10 копеек, причем бутылка на 9 копеек дороже пробки. Сколько стоит бутылка без пробки?
3. Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?
4. Из бочки вина перелили ложку его в (неполный) стакан с чаем. А потом такую же ложку (неоднородной) смеси из стакана – обратно в бочку. Теперь и в бочке, и в стакане имеется некоторый объем посторонней жидкости (вина в стакане, чая в бочке). Где объем посторонней жидкости больше: в стакане или в бочке?
5. Из A в B и из B в A на рассвете (одновременно) вышли навстречу друг другу (по одной дороге) две старушки. Они встретились в полдень, но не остановились, а каждая продолжала идти с той же скоростью, и первая пришла (в B) в 4 часа дня, а вторая (в A) в 9 часов вечера. В котором часу был в этот день рассвет?
6. Гипотенуза прямоугольного треугольника (в американском стандартном экзамене) – 10 дюймов, а опущенная на нее высота – 6 дюймов. Найти площадь треугольника. С этой задачей американские школьники успешно справлялись 10 лет, но потом приехали из Москвы русские школьники, и ни один эту задачу решить, как американские школьники (дававшие ответ 30 квадратных дюймов), не мог. Почему?
7. У Васи сестер на 2 больше, чем братьев. На сколько у Васиных родителей больше дочерей, чем сыновей?
8. В Южной Америке есть круглое озеро, где 1 июня каждого года в центре озера появляется цветок Виктории Регии (стебель поднимается со дна, а лепестки лежат на воде, как у кувшинки). Каждые сутки площадь цветка увеличивается вдвое, и 1 июля он, наконец, покрывает все озеро, лепестки осыпаются, семена опускаются на дно. Какого числа площадь цветка составляет половину площади озера?
9. Волк, коза и капуста должны быть перевезены мужиком через реку в лодке, но лодка столь мала, что он может брать с собой только один из трех грузов. Как перевезти все три груза (волка нельзя оставлять наедине с козой, а козу – с капустой) через реку?
10. Улитка за день залезает вверх по столбу на 3 см, а за ночь, уснув, нечаянно спускается на 2 см. Высота столба 10 м, а наверху лежит вкусная для улитки конфета. Через сколько дней улитка ее достанет?
11. Охотник прошел от своей палатки 10 км на юг, повернул на восток, прошел прямо на восток еще 10 км, убил медведя, повернул на север и, пройдя еще 10 км, оказался у палатки. Какого цвета был медведь и где это все было?
12. Сегодня в 12 часов дня был прилив. Когда он будет (там же) завтра?
13. На книжной полке рядом стоят два тома Пушкина: первый и второй. Страницы каждого тома имеют вместе толщину 2 см, а обложка – каждая – 2 мм. Червь прогрыз (перпендикулярно страницам) от первой страницы первого тома до последней страницы второго тома. Какой путь он прогрыз?
14. Найти тело, имеющее такой вид сверху и такой вид спереди (многогранники). Нарисовать вид сбоку (невидимые ребра многогранника изобразить пунктиром). 
15. Сколькими способами можно разбить число 64 на 10 натуральных слагаемых (целых > 0), наибольшее из которых равно 12?  Разбиения, отличающиеся только порядком слагаемых, не считаются при подсчете числа разбиений разными.
16. Положив (нужным образом) друг на друга несколько одинаковых пластинок (например, костяшек домино), можно образовать навес длиной x костяшек. Каково наибольшее достижимое значение длины навеса x? 
17. От города A до города B расстояние 40 км. Два велосипедиста выехали из A и из B одновременно и навстречу друг другу, один со скоростью 10 км/час, а другой – 15 км/час. Муха вылетела с первым из A со скоростью 100 км/час, долетела до второго, села ему на лоб и полетела обратно к первому, села ему на лоб, вернулась ко второму и так далее, пока они не столкнулись лбами и не раздавили ими муху. Сколько километров она пролетела всего? 
18. Одна костяшка домино покрывает две клетки шахматной доски. Покрыть 31 костяшкой все клетки, кроме двух противоположных (на одной диагонали). Шахматная доска состоит из 8 × 8 = 64 клеток. 
19. Гусеница хочет проползти из одного угла кубической комнаты (на полу слева) в противоположный (на потолке справа). Найти кратчайший путь такого путешествия по стенам комнаты. 
20. Имея два сосуда объемом 5 литров и 3 литра, отмерь один литр (получи его в одном из сосудов).
21. В семье пять голов и четырнадцать ног. Сколько из них людей, а сколько собак?
22. На сторонах треугольника ABC во внешнюю сторону от него построены равносторонние треугольники (со сторонами AB, BC, CA). Доказать, что их центры (∗) образуют равносторонний треугольник. 
23. Какие многоугольники могут получиться при пересечении куба плоскостью? Может ли получиться пятиугольник? Семиугольник? Правильный шестиугольник?
24. Через центр куба провести прямую так, чтобы сумма квадратов расстояний восьми вершин куба от нее была а) максимальной, б) минимальной (по сравнению с другими прямыми).
25. Прямой круговой конус пересечен плоскостью по замкнутой кривой. Вписанные в конус шары касаются плоскости сечения в точках A для одного и B для другого шара. Найти на линии сечения точку C так, чтобы сумма расстояний CA + CB была а) наибольшей, б) наименьшей. 
26. На цилиндр, образованный касательными к меридианам в точках экватора земного шара, поверхность Земли спроектирована лучами, параллельными экватору и проходящими через (соединяющую полюса) ось земли. Будет ли площадь проекции Франции больше или меньше, чем площадь самой Франции? 
27. Доказать, что остаток от деления числа 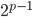$2^{p-1}$ на простое нечетное число $p$ равен 1 (примеры: $2^2=3a+1$, $2^4=5b+1$, $2^6=7c+1$, $2^{10}-1=1023=11\cdot93$).
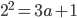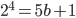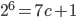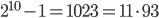28. Иголку длиной 10 см случайно бросают на разлинованную бумагу, где расстояние между соседними линиями тоже 10 см, повторяя это N (миллион) раз. Сколько раз (примерно, с ошибкой в несколько процентов) упавшая иголка пересечет линию бумаги? 
29. Многогранники с треугольными гранями – это, например, платоновы тела, тетраэдр (4 грани), октаэдр (их 8), икосаэдр (их 20 – и все грани одинаковые; интересно его нарисовать, у него 12 вершин и 30 ребер). Верно ли, что для любого такого (ограниченного выпуклого многогранника с треугольными гранями) число граней равно удвоенному числу вершин минус четыре?
30. Додекаэдр – выпуклый многогранник с двенадцатью (правильными) пятиугольными гранями, двадцатью вершинами и тридцатью ребрами (его вершины – это центры граней икосаэдра). Вписать в додекаэдр пять кубов (вершины каждого куба – часть вершин додекаэдра), ребра которых – диагонали граней додекаэдра (ребер у куба 12, по одной на грани). Это придумал Кеплер, ради планет. 
31. а) Найти пересечение двух тетраэдров, вписанных в куб (так, что вершины каждого – часть вершин куба, а ребра – диагонали граней). Какую часть объема куба составляет это пересечение тетраэдров? б)  Построить сечение куба плоскостью, проходящей через три заданные точки на ребрах, то есть нарисовать многоугольник, по которому плоскость сечения пересекает грани куба. 
32. Сколько симметрий имеет тетраэдр? куб? октаэдр? икосаэдр? додекаэдр? Симметрия – это преобразование, сохраняющее длины.
33. Сколькими способами можно раскрасить 6 граней одинаковых кубиков шестью красками (1, ..., 6) (по одной на грани) так, чтобы никакие два из получившихся раскрашенных кубиков не были одинаковыми (не переходили один в другой при каком-то вращении)?
34. Сколькими разными способами можно переставить n предметов? Для n = 3 их шесть: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). А если предметов n = 4? n = 5? n = 6? n = 10?
35. У куба 4 большие диагонали. Сколько разных перестановок этих четырех предметов осуществляют все вращения куба?
36. Из куба суммы нескольких целых чисел вычли сумму кубов этих чисел. Верно ли, что разность всегда делится на 3?
37. Такой же вопрос для пятых степеней и делимости на 5, седьмых степеней и делимости на 7.

смотрите раздел Математика