ЕГЭ по математике 2015
Решение тренировочной работы от 22 апреля 2015 МИОО
Профильный уровень
условия задач здесь
Решение задач (в процессе)
- Решение с сайта www.itmathrepetitor.ru. Если покупать подписку, то за полгода требуется заплатить 830 р, без подписки за 25 журналов придется заплатить
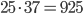 р. Значит, разница составляет
р. Значит, разница составляет 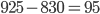 р.
р. - Находим на оси абсцисс (горизонтальной оси) точку, соответствующую числу 1. Из этой точки восстанавливаем перпендикуляр до пересечения с графиком в точке А. Из точки А опускаем перпендикуляр на ось ординат (вертикальную ось). По точке пересечения это перпендикуляра и определяем ответ. Решение с сайта www.itmathrepetitor.ru.
- Решение с сайта www.itmathrepetitor.ru. Вероятность того, что чайник прослужит не более двух лет, равна
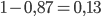 . Вероятность того, что чайник прослужит не более одного года, равна
. Вероятность того, что чайник прослужит не более одного года, равна 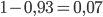 . Тогда искомая вероятность равна
. Тогда искомая вероятность равна 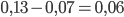 , так как
, так как 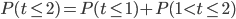 .
. - Сократим знаменатели с левой и правой частях (при этом теряем ограничение
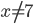 , которое проверим в конце решения). Тогда
, которое проверим в конце решения). Тогда 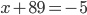 и
и  , что не равно
, что не равно 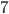 .
. - Рассмотрим треугольник AOC (см. рис). Угол АОС является центральным (точка О - центр окружности), поэтому угол АВС в два раза меньше угла АОС. Так как ОС - диагональ квадрата 2 х 2, то угол ОСА равен 45о, а угол АОС прямой. Поэтому угол АВС равен 90/2 = 45 градусов.

- Решение с сайта www.itmathrepetitor.ru. После вынесения
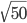 за скобки, применим формулу двойного угла для косинуса. Тогда
за скобки, применим формулу двойного угла для косинуса. Тогда 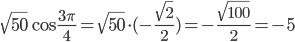 . Заметим, что по формулам приведения
. Заметим, что по формулам приведения 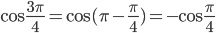 .
. - Решение с сайта www.itmathrepetitor.ru. Гипотенуза основания равна
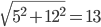 (по теореме Пифагора). Тогда по формуле
(по теореме Пифагора). Тогда по формуле 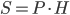 , где
, где 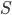 - площадь боковой поверхности прямой призмы,
- площадь боковой поверхности прямой призмы, 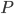 - периметр основания,
- периметр основания, 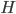 - высота призмы, получаем, что
- высота призмы, получаем, что 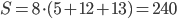 , так как в прямой призме боковое ребро является высотой.
, так как в прямой призме боковое ребро является высотой. - Решение с сайта www.itmathrepetitor.ru. Средняя скорость может быть найдена как отношение всего пути к отношению потраченного времени, то есть
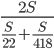 . После сокращения
. После сокращения 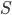 - расстояния в одну сторону путешествия и упрощения, получаем
- расстояния в одну сторону путешествия и упрощения, получаем 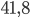 .
. - Решение с сайта www.itmathrepetitor.ru. Производная функции
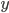 равна
равна 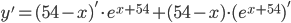
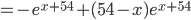 . Приравняем ее к нуля и сократим
. Приравняем ее к нуля и сократим 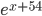 . Тогда
. Тогда 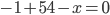 , откуда
, откуда  . Осталось исследовать знаки производной в окрестности найденной точки.
. Осталось исследовать знаки производной в окрестности найденной точки. - a) Решение с сайта www.itmathrepetitor.ru. Применим формулу двойного угла для косинуса, получим уравнение
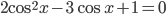 , которое является квадратным относительно
, которое является квадратным относительно  .
.
Решив его, получим, что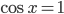 или
или 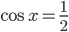 . Откуда
. Откуда 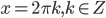 и
и 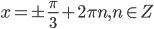 .
.
б) Представим найденное в пункте а) решение в виде трех формул . Далее решаем три неравенства
. Далее решаем три неравенства 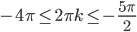 ,
, 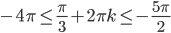 и
и 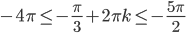 . Получаем
. Получаем 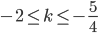 ,
, 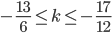 и
и 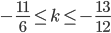 . Так как
. Так как 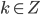 , то есть
, то есть 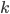 - целое число, то
- целое число, то 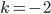 для первого неравенства,
для первого неравенства, 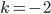 для второго неравенства, для третьего неравенства целых значений
для второго неравенства, для третьего неравенства целых значений 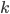 не существует.
не существует.
Осталось подставить каждое из найденных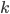 в свою формулу и вычислить конкретные углы.
в свою формулу и вычислить конкретные углы. - Решение с сайта www.itmathrepetitor.ru. Заметим, что
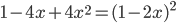 . Тогда числитель можно записать как
. Тогда числитель можно записать как 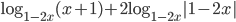 . Так как
. Так как 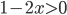 , то
, то 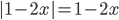 и числитель равен
и числитель равен 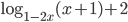 . Пусть
. Пусть 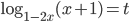 , тогда
, тогда 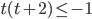
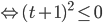 . Так как квадрат неотрицателен для любого
. Так как квадрат неотрицателен для любого 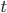 , то
, то 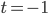 . Поэтому
. Поэтому 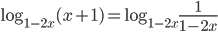 и
и 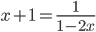 , откуда
, откуда 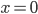 или
или 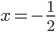 . После проверки получаем, что
. После проверки получаем, что 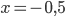 .
. - Треугольник ATB подобен треугольнику THC, треугольник TBH подобен треугольнику DTC. Поэтому
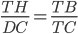 и
и 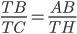 . Значит,
. Значит, 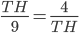 , откуда
, откуда 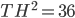 и
и 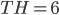 . Решение с сайта www.itmathrepetitor.ru.
. Решение с сайта www.itmathrepetitor.ru.
смотрите еще ЕГЭ 2015 Демонстрационный вариант (профильный уровень)
