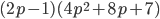7. Представьте число 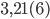 в виде обыкновенной дроби.
в виде обыкновенной дроби.
Решение:
Пусть 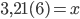 . Для того чтобы “,” оказалась перед периодом (6) умножим левую и правую части этого равенства на 100:
. Для того чтобы “,” оказалась перед периодом (6) умножим левую и правую части этого равенства на 100: 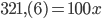 . И еще умножим на 10, чтобы “,” сместилась на длину периода:
. И еще умножим на 10, чтобы “,” сместилась на длину периода: 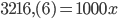 . Отнимем от последнего уравнения предыдущее:
. Отнимем от последнего уравнения предыдущее: 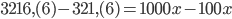 , и заметим, что в левой части получается целое число:
, и заметим, что в левой части получается целое число: 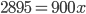 , откуда
, откуда 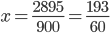 .
.
Ответ: 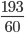
8. 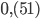 . Ответ:
. Ответ: 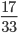
9. 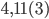 . Ответ:
. Ответ: 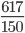
10. Раскройте скобки и приведите подобные слагаемые в выражении 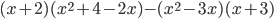 .
.
Решение:
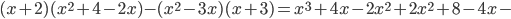
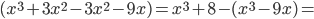
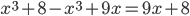 .
.
Ответ: 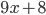
11. 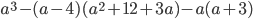 . Ответ:
. Ответ: 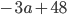
12. 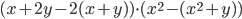 . Ответ:
. Ответ: 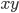
13. Разложите на множители выражение 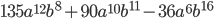 .
.
Решение:
Так как среди степеней выражений 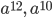 и
и 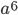 наименьшая степень равна 6; среди степеней выражений
наименьшая степень равна 6; среди степеней выражений 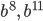 и
и 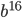 наименьшая равна 8 и наибольший общий делитель чисел 135, 90 и 36 равен 9, то общий множитель равен
наименьшая равна 8 и наибольший общий делитель чисел 135, 90 и 36 равен 9, то общий множитель равен 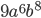 . Тогда
. Тогда 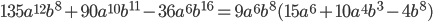 .
.
Ответ: 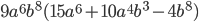
14. 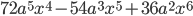 . Ответ:
. Ответ: 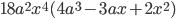
15. 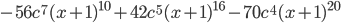 .
.
Ответ: 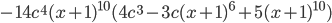
16. Разложите на множители выражение 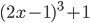 .
.
Решение:
Применим формулу сокращенного умножения 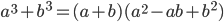
при 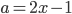 и
и 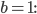
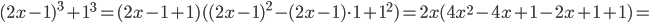
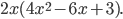 Ко второму множителю нельзя применить формулу разложения квадратного трехчлена
Ко второму множителю нельзя применить формулу разложения квадратного трехчлена 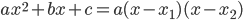 , так как дискриминант равен
, так как дискриминант равен 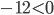 .
.
Ответ: 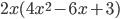
17. 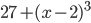 . Ответ:
. Ответ: 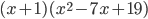
18. 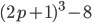 . Ответ:
. Ответ: