ЕГЭ 2016 Пробный вариант Томск
Профильный 11 класс
 Диагностическая работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развернутым ответом.
Диагностическая работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развернутым ответом.
На выполнение диагностической работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1-12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1. При выполнении заданий 13—19 требуется записать полное решение и ответ в бланк ответов № 2.
Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются.
Желаем успеха!
Условия задач
Часть 1
- Розничная цена учебника 330 рублей, она на 10% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 15000 рублей?
- На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.

- Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.

- На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,3. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
- Найдите корень уравнения
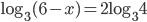
- Боковая сторона равнобедренного треугольника равна 5, а основание равно 8. Найдите площадь этого треугольника.
- На рисунке изображен график
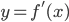 - производной функции
- производной функции 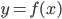 , определенной на интервале (-7;14). Найдите количество точек максимума функции
, определенной на интервале (-7;14). Найдите количество точек максимума функции 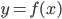 , принадлежащих отрезку [-6;9]
, принадлежащих отрезку [-6;9] 
- Длина окружности основания конуса равна 4, образующая равна 3. Найдите площадь боковой поверхности конуса.
Часть 2
- Найдите
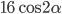 , если
, если 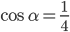
- Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием
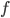 = 30 см. Расстояние
= 30 см. Расстояние 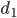 от линзы до лампочки может изменяться в пределах от 40 до 65 см, а расстояние
от линзы до лампочки может изменяться в пределах от 40 до 65 см, а расстояние 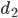 от линзы до экрана — в пределах от 75 до 100 см. Изображение на экране будет чётким, если выполнено соотношение
от линзы до экрана — в пределах от 75 до 100 см. Изображение на экране будет чётким, если выполнено соотношение 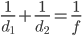 . Укажите, на каком наибольшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.
. Укажите, на каком наибольшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах. - Теплоход проходит по течению реки до пункта назначения 300 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 50 часов после отплытия из него. Ответ дайте в км/ч.
- Найдите наименьшее значение функции
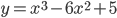 на отрезке [1;5]
на отрезке [1;5] - а) Решите уравнение
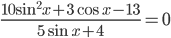 б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Найдите все корни этого уравнения, принадлежащие отрезку ![[5\pi;6,5\pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_d3644c0afdb6e2578a84d53716176d54.gif)
- Дан прямой круговой конус с вершиной М. Осевое сечение конуса — треугольник с углом 120° при вершине М. Образующая конуса равна
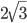 . Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
. Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник — тупоугольный.
б) Найдите расстояние от центра О основания конуса до плоскости сечения. - Решите уравнение
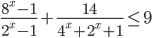
- Окружность с центром О касается боковой стороны АВ равнобедренного треугольника ABC, продолжения боковой стороны АС и продолжения основания ВС в точке N. Точка М — середина основания ВС.
а) Докажите, что MN = АС.
б) Найдите ОС, если стороны треугольника ABC равны 5, 5 и 8. - Бизнес-проект «А» предполагает в течение первых двух лет рост вложенных в него сумм на 34,56% ежегодно и на 44% ежегодно в течение следующих двух лет. Проект «Б» предполагает рост на постоянное целое число n процентов ежегодно. Найдите наименьшее значение n, при котором за первые четыре года проект «Б» будет выгоднее проекта «А».
- Найдите все значения параметра
 ,
, 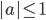 , при каждом из которых система уравнений
, при каждом из которых система уравнений 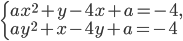 имеет единственное решение
имеет единственное решение - Аня играет в игру: на доске написаны два различных натуральных числа
 и
и  , оба меньше 1000. Если
, оба меньше 1000. Если 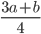 и
и 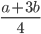 оба натуральные, то Аня делает ход — заменяет этими двумя числами предыдущие. Если хотя бы одно из этих чисел не является натуральным, то игра прекращается.
оба натуральные, то Аня делает ход — заменяет этими двумя числами предыдущие. Если хотя бы одно из этих чисел не является натуральным, то игра прекращается.
а) Может ли игра продолжаться ровно три хода?
б) Существуют ли два начальных числа таких, что игра будет продолжаться не менее 9 ходов?
в) Аня сделала первый ход в игре. Найдите наибольшее возможное отношение произведения полученных двух чисел к произведению
смотрите также Досрочный ЕГЭ по математике 2015
Ответы
(скоро...)
Как скоро появятся ответы? Хотелось бы уже проверить
пишите свои ответы. на этой неделе проверю что-нибудь