Решение олимпиады МФТИ 2015 11 класс
Условия задач здесь
Вариант 11
- Возьмем логарифм по основанию 2 от обеих частей уравнения. Тогда
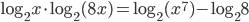 , что равносильно
, что равносильно 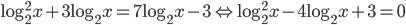 , откуда
, откуда 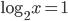 или
или 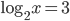 , то есть
, то есть 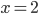 или
или 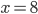 .
. - Преобразуем правую часть уравнения
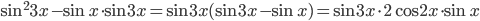
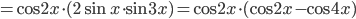 =
= 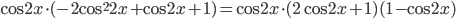 . Пусть
. Пусть 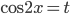 . Тогда
. Тогда 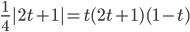 .
.
Рассмотрим три случая.
а)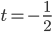 . Тогда
. Тогда 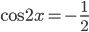
б)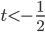 . Тогда
. Тогда 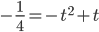 и
и 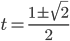 . Оба значения не удовлетворяют условию
. Оба значения не удовлетворяют условию 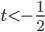
в)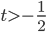 . Тогда
. Тогда 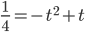 и
и 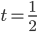 .
.
В результате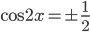 и
и 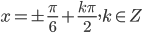
- Так как
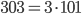 , то одно из чисел
, то одно из чисел 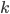 или
или 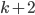 делится на
делится на  . Рассмотрим два случая.
. Рассмотрим два случая.
а)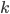 делится на
делится на  , то есть
, то есть 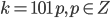 . Тогда
. Тогда 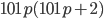 делится на
делится на 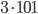 , то есть
, то есть 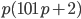 делится на 3. Первый множитель делится на 3 при
делится на 3. Первый множитель делится на 3 при 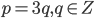 , а второй - при
, а второй - при 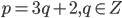 , откуда
, откуда 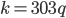 ,
, 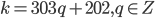 .
.
б) Если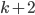 делится на 101, то
делится на 101, то 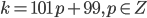 и
и 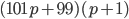 делится на 3. Первый множитель делится на 3 при
делится на 3. Первый множитель делится на 3 при 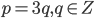 , а второй - при
, а второй - при 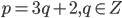 , откуда получаем, что
, откуда получаем, что 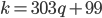 ,
, 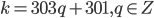 .
.
Итак, условию задачи удовлетворяют числа, дающие остатки 0, 202, 99, 301 при делении на 303, то есть подходят каждые 4 из 303 подряд идущих чисел. Так как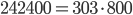 , получаем
, получаем 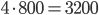 чисел.
чисел.
