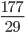Тренировочная работа МИОО
24 сентября 2015 г
Условия задач, ответы и решения
13. а) Решите уравнение  ; Решение
; Решение
б) Найдите все корни этого уравнения, принадлежащие отрезку ![[-3\pi; -3\pi/2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4029140917fa79c7e0488f25f50cd403.gif) Решение
Решение
14. На ребре 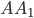 прямоугольного параллелепипеда
прямоугольного параллелепипеда 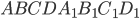 взята точка
взята точка 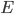 так, что
так, что 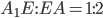 , на ребре
, на ребре 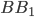 - точка
- точка 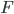 так, что
так, что 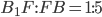 , а точка
, а точка 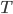 - середина ребра
- середина ребра 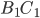 . Известно, что
. Известно, что 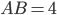 ,
, 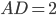 и
и 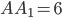 . а) Докажите, что плоскость
. а) Докажите, что плоскость 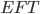 проходит через вершину
проходит через вершину 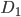 . б) Найдите угол между плоскостью
. б) Найдите угол между плоскостью 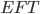 и плоскостью
и плоскостью 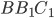 .
.
15.1 Решите неравенство 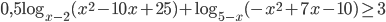 Решение
Решение
15.2 Решите неравенство 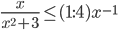 Решение
Решение
16. Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN.
а) Докажите, что четырёхугольник NQOH — параллелограмм.
б) Найдите KN , если угол LKN = 750 и LM = 1
17. Производство  тыс. единиц продукции обходится в
тыс. единиц продукции обходится в 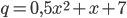 млн. рублей в год. При цене
млн. рублей в год. При цене  тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн. рублей) составляет
тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн. рублей) составляет 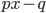 . При каком наименьшем значении
. При каком наименьшем значении  через три года суммарная прибыль составит не менее 75 млн. рублей? Решение
через три года суммарная прибыль составит не менее 75 млн. рублей? Решение
18. Найдите все целочисленные значения параметра  , при каждом из которых система
, при каждом из которых система 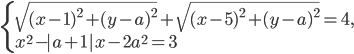 имеет единственное решение.
имеет единственное решение.
19. Известно, что 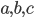 и
и 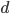 - попарно различные положительные двузначные числа.
- попарно различные положительные двузначные числа.
а) Может ли выполняться равенство 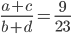 ?
?
б) Может ли дробь 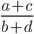 быть в 11 раз меньше, чем сумма
быть в 11 раз меньше, чем сумма 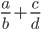 ?
?
в) Какое наименьшее значение может принимать дробь 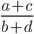 , если
, если 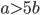 и
и 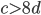 ?
?
@СтатГрад
смотрите еще Демонстрационный вариант КИМ для проведения в 2016 году ЕГЭ по математике 11 класс Профильный уровень
Ответы
- а)
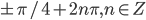 б)
б)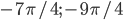
- б)
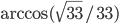
- 1)
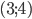 2)
2) ![(-\infty; -1]\cup (0;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_0106db2b807f8fdd7495011e4a091fa6.gif)
- б) 3
- p=9
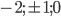
- а) да б) нет в)