Варианты вступительных экзаменов по математике в МГУ. Высшая школа бизнеса.
Высшая школа бизнеса МГУ, 2003 г.
- Решите неравенство
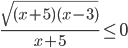 .
. - В банке общая сумма кредитов, выданная населению, составляет 25% от суммы кредитов, выданных предприятиям. Какой процент от общего объема кредитования в этом банке приходится на долю предприятий?
- Решите уравнение
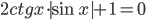 .
. - Решите систему уравнений
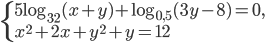 .
. - Найдите стороны параллелограмма ABCD, если известны координаты двух его противоположных вершин А(-3; -6), C(5; 12) и точки N(1; 9), являющейся серединой стороны BC.
- Найдите все пары целых чисел (x; y), удовлетворяющих уравнению
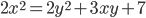 .
. - В равнобедренном треугольнике ABC (AB = BC) угол при вершине B равен 80о, а точка M внутри треугольника расположена так, что угол MAC равен 30о, а угол MCA равен 10о. Найдите величину угла BMC.
- Найдите все значения параметра
 , при которых уравнение
, при которых уравнение 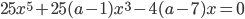 имеет ровно 5 различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
имеет ровно 5 различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
Высшая школа бизнеса МГУ, 2004 г.
- Решите неравенство
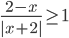 .
. - Решите уравнение
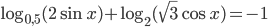 .
. - Решите систему уравнений
![\left\{\begin{array}{l l} \sqrt[3]{x-1}-\sqrt[3]{y+2}=1,\\x-y=22\end{array}\right.](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_1f0d40b7f3abd428c3ba32f911f8034f.gif) .
. - Найдите периметр треугольника KLM, если известны координаты его вершин K(-4; -3), L(2; 5) и точки P(5; 1), являющейся серединой стороны LM.
- Сколько времени в течение суток на электронном табло вокзальных часов, которые показывают время в диапазоне от 00:00 до 23:59, присутствует хотя бы одна цифра 5?
- Найдите все пары целых неотрицательных чисел
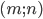 , являющихся решениями уравнения
, являющихся решениями уравнения 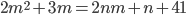 .
. - Найдите наименьшее значение выражения
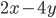 на множестве переменных x, y, удовлетворяющих условию
на множестве переменных x, y, удовлетворяющих условию 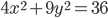 .
. - Найдите все значения параметра
![a\in [-6;6]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c24b630ae230e0b9096db879255e6912.gif) , при которых неравенство
, при которых неравенство 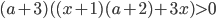 выполняется при любых
выполняется при любых 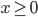 .
.
Ответы
2003 г
- x<-5, x=3
- 80%
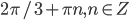
- x=-2, y=3
- AB = 12, BC = 10
- x=3, y=1; x=-3, y=-1
- 70o
- -2
2004 г
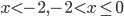
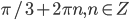
- (28; 6), (-7; -29)
- 32
- 7 час 30 мин
- (10; 9)
- -10
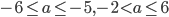 .
.