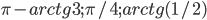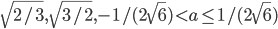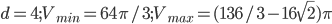Варианты вступительных экзаменов в МФТИ 2007 г. по математике
Вариант 1
- Решите уравнение
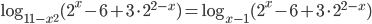 .
. - Решите уравнение
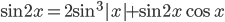 .
. - Решите неравенство
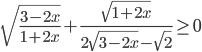 .
. - Окружности
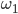 и
и 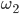 лежат внутри треугольника ABC, в котором AB = BC = a = 6, AC = 2, а радиус
лежат внутри треугольника ABC, в котором AB = BC = a = 6, AC = 2, а радиус 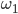 в два раза больше радиуса
в два раза больше радиуса 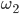 . Окружности
. Окружности 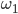 и
и 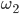 касаются внешним образом, причем
касаются внешним образом, причем 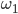 касается сторон AB и AC, а
касается сторон AB и AC, а 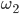 - сторон BC и AC треугольника ABC. Найдите радиус окружности
- сторон BC и AC треугольника ABC. Найдите радиус окружности 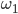 , если a = 6. Найдите все значения a, при которых существуют указанные окружности.
, если a = 6. Найдите все значения a, при которых существуют указанные окружности. - Найдите все значения параметра
 , при которых наибольшее значение величины
, при которых наибольшее значение величины 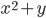 на множестве пар действительных чисел
на множестве пар действительных чисел 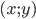 , удовлетворяющих одновременно двум неравенствам
, удовлетворяющих одновременно двум неравенствам 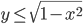 и
и 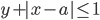 , будет максимально возможным. Найдите это максимально возможное значение.
, будет максимально возможным. Найдите это максимально возможное значение. - В прямоугольном параллелепипеде ABCDA1B1C1D1 четыре числа - длины ребер и диагонали АС1 - образуют арифметическую прогрессию с положительной разностью d, причем AA1<AB<BC. Две внешне касающиеся друг друга сферы одинакового неизвестного радиуса R расположены так, что их центры лежат внутри параллелепипеда, причем первая сфера касается граней ABB1A1, ADD1A1, ABCD, а вторая - граней BCC1B1, CDD1C1, A1B1C1D1. Найдите: а) длины ребер параллелепипеда; б) угол между прямыми CD1 и AC1; в) радиус R.
Вариант 5
- Решите уравнение
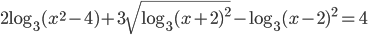 .
. - Решите уравнение
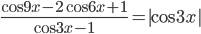 .
. - Решите неравенство
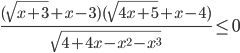 .
. - Окружность
 с центром в точке O на стороне АС треугольника АВС касается сторон АВ и ВС в точках D и E соответственно. Известно, что AD = 2CE, а угол DOE равен arctg (1/3). Найдите углы треугольника ABC и отношение его площади к площади круга, ограниченного окружностью
с центром в точке O на стороне АС треугольника АВС касается сторон АВ и ВС в точках D и E соответственно. Известно, что AD = 2CE, а угол DOE равен arctg (1/3). Найдите углы треугольника ABC и отношение его площади к площади круга, ограниченного окружностью  .
. - Найдите все значения параметра
 , при которых существует ровно две пары действительных чисел
, при которых существует ровно две пары действительных чисел 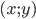 , удовлетворяющих системе уравнений
, удовлетворяющих системе уравнений 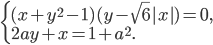
- Внутри прямоугольного параллелепипеда ABCDA1B1C1D1 расположены два шара
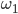 и
и 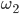 , касающиеся друг друга внешним образом. Кроме того, шар
, касающиеся друг друга внешним образом. Кроме того, шар 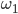 касается граней ABCD, ABB1A1, ADD1A1, а шар
касается граней ABCD, ABB1A1, ADD1A1, а шар 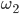 касается граней A1B1C1D1, BCC1B1, CDD1C1. Известно, что AB =
касается граней A1B1C1D1, BCC1B1, CDD1C1. Известно, что AB = 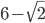 , A1D1 =
, A1D1 = 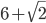 , CC1 = 6. Найдите расстояние между центрами шаров. Найдите наибольший и наименьший суммарный объем шаров.
, CC1 = 6. Найдите расстояние между центрами шаров. Найдите наибольший и наименьший суммарный объем шаров.
Ответы
Вариант 1
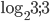
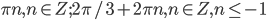
- (-1/2; 5/4)
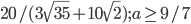
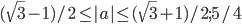
- а)
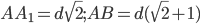 ; б)
; б) 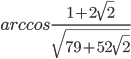 ; в)
; в) 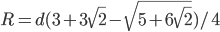 .
.
Вариант 5
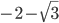
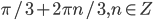
- 1