Всероссийская олимпиада по математике 2016.
Школьный этап

к разделу Олимпиадные задачи

Условия задач для 9-11 классов

9 класс

1. Натуральное число называется палиндромом, если оно не изменяется при записывании его цифр в обратном порядке (например, 626 — палиндром, а 2015 — нет). Представьте число 2015 в виде суммы двух палиндромов.

2. На доске была написана несократимая дробь. Петя уменьшил её числитель на 1, а знаменатель на 2. А Вася прибавил к числителю 1, а знаменатель оставил без изменений. Оказалось, что в результате мальчики получили одинаковые значения. Какой именно результат у них мог получиться?
3. Дима должен был попасть на станцию в 18:00. К этому времени за ним должен был приехать отец на автомобиле. Однако Дима успел на более раннюю электричку и оказался на станции в 17:05. Он не стал дожидаться отца и пошёл ему навстречу. По дороге они встретились, Дима сел в автомобиль, и они приехали домой на 10 минут раньше рассчитанного времени. С какой скоростью шёл Дима до встречи с отцом, если скорость автомобиля была 60 км/ч?
4. В подземном царстве живут гномы, предпочитающие носить либо зелёные, либо синие, либо красные кафтаны. Некоторые из них всегда лгут, а остальные всегда говорят правду. Однажды каждому из них задали четыре вопроса.
   1. «Ты предпочитаешь носить зелёный кафтан?»
   2. «Ты предпочитаешь носить синий кафтан?»
   3. «Ты предпочитаешь носить красный кафтан?»
   4. «На предыдущие вопросы ты отвечал честно?»
   На первый вопрос «да» ответили 40 гномов, на второй — 50, на третий — 70, а на четвёртый — 100. Сколько честных гномов в подземном царстве?
5. В треугольнике АВС медиана, выходящая из вершины А, перпендикулярна биссектрисе угла В, а медиана, выходящая из вершины В, перпендикулярна биссектрисе угла А. Известно, что сторона АВ = 1. Найдите периметр треугольника АВС.
6. Есть три сосуда объёмом 3 л, 4 л и 5 л без делений, кран с водой, раковина и 3 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 6 л смеси воды с сиропом так, чтобы в каждом сосуде количество воды было равно количеству сиропа?

10 класс

1. В таблице 3 х 3 записаны числа, как показано на рисунке. За ход разрешается
   выбрать три клетки в форме трёхклеточного уголка и уменьшить число в каждой из них на 1. Покажите, как такими операциями сделать таблицу, в которой во всех клетках стоят нули. 
2. Делится ли число 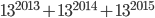\(13^{2013}+13^{2014}+13^{2015}\) на \(61\)?
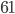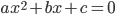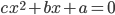3. Даны два уравнения \(ax^2+bx+c=0\) и \(cx^2+bx+a=0\), в которых все коэффициенты ненулевые. Оказалось, что они имеют общий корень. Верно ли, что \(a=c\)?
4. В некоторой школе каждый десятиклассник либо всегда говорит правду, либо всегда лжёт. Директор вызвал к себе нескольких десятиклассников и спросил каждого из них про каждого из остальных, правдивец тот или лжец. Всего было получено 44 ответа «правдивец» и 28 ответов «лжец». Сколько правдивых ответов мог получить директор?
5. Могут ли две биссектрисы треугольника разбивать его на четыре части равной площади?
6. Существует ли натуральное число, кратное 2015, сумма цифр которого равна 2015?

11 класс

1. За лето однокомнатная квартира подорожала на 21 %, двухкомнатная — на 11 %, а суммарная стоимость квартир — на 15 %. Во сколько раз однокомнатная квартира дешевле двухкомнатной?
2. Найдите какую-нибудь пару натуральных чисел a и b, бóльших 1, удовлетворяющих уравнению \(a^{13}\cdot b^{31}=6^{2015}\).
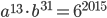3. Может ли сумма 2015 последовательных натуральных чисел оканчиваться той же цифрой, что и сумма следующих 2019 чисел?
4. Учительница Мария Ивановна готовит задания для урока математики. Она хочет в уравнении 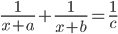\(\displaystyle\frac{1}{x+a}+\frac{1}{x+b}=\frac{1}{c}\) вместо a, b и c поставить три различных натуральных числа, чтобы корни уравнения были целыми числами. Помогите ей: подберите такие числа и решите уравнение.
5. Петя на ребре AB куба ABCDA₁B₁C₁D₁ отметил точку X, делящую ребро AB в отношении 1 : 2, считая от вершины A. Приведите пример, как Петя может отметить на рёбрах CC₁ и A₁D₁ соответственно точки Y и Z, чтобы треугольник XYZ был равносторонним. Пример обоснуйте.
6. В турнире по шашкам участвовали ученики 10 и 11 классов. Каждый сыграл с каждым один раз. За победу участник получал 2 очка, за ничью — 1 очко, за проигрыш — 0 очков. Одиннадцатиклассников было в 10 раз больше, чем десятиклассников, и они вместе набрали в 4,5 раза больше очков, нежели все десятиклассники. Сколько очков набрал самый успешный десятиклассник?

к разделу Олимпиадные задачи