Элементарное введение в Wolfram Language

(язык программирования системы Mathematica)

перейти к содержанию

5. Операции над списками

В Wolfram Language функции для работы со списками исчисляются тысячами.

Вы можете выполнять арифметические действия над списками:
ln[1]:={1,2,3}+10
Out[1]={11,12,13}
ln[1]:={1,1,2}*{1,2,3}
Out[1]={1,2,6}


| То есть перемножаются соответствующие элементы: {1$\cdot$1, 1$\cdot$2, 2$\cdot$3}

Можете найти квадраты первых 10 натуральных чисел:
ln[1]:=Range[10]^2
Out[1]={1,4,9,16,25,36,49,64,81,100}


Построить график квадратов первых 20 натуральных чисел:
ln[4]:=ListPlot[Range[20]^2]


Вы можете выполнять арифметические действия над списками:
ln[1]:={1,2,3}+10
Out[1]={11,12,13}


Функция Sort упорядочивает список:
ln[1]:=Sort[{4,2,1,3,6}]
Out[1]={1,2,3,4,6}


Функция Length определяет длину списка:
ln[1]:=Length[{5,3,4,5,3,4,5}]
Out[1]=7


Функция Total находит сумму всех элементов списка:
ln[1]:=Total[{1,1,2,2}]
Out[1]=6


| Кстати, Total[{1, 2, 3, a}] равен 6+a.

Найти сумму целых чисел от 1 до 10 включительно можно так:
ln[1]:=Total[Range[10]]
Out[1]=55


Функция Count опредеяет количество вхождений элемента в список.

Количество вхождений элемента a в список:
ln[1]:=Сount[{a,b,a,a,c,b,a},a]
Out[1]=4


Часто бывает необходимо извлечь из списка элемент на заданной позиции. Функция First возвращает первый элемент, функция Last - последний элемент, функция Part возвращает элемент на заданной в параметрах позиции.

Извлечение первого элемента:
ln[1]:=First[{7,6,5}]
Out[1]=7


Извлечение последнего элемента:
ln[1]:=Last[{7,6,5}]
Out[1]=5


Извлечение элемента на второй позиции:
ln[1]:=Part[{7,6,5},2]
Out[1]=6


Извлечение первого элемента из упорядоченного по возрастанию списка равносильно поиску минимального элемента списка:
ln[1]:=First[Sort[{6,7,1,2,4,5}]]
Out[1]=1


ln[1]:=Min[{6,7,1,2,4,5}]
Out[1]=1


Вы можете создать список из цифр данного целого числа с помощью функции IntegerDigits.

Создание списка цифр из числа:
ln[1]:=IntegerDigits[1988]
Out[1]={1,9,8,8}


| Для IntegerDigits[-1988] результат аналогичен. Вариант IntegerDigits[1988.3]выбрасывает ошибку.

Функция Take позволяет сформировать новый список из первых элементов данного списка.

Получение списка из первых трех элементов:
ln[1]:=Take[{101,203,401,602,332,412},3]
Out[1]={101,203,401}


Получение списка из первых десяти цифр числа 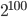$2^{100}$:
ln[1]:=First[IntegerDigits[2^100],10]
Out[1]={1,2,6,7,6,5,0,6,0,0}


Для удаления первых элементов списка воспользуйтесь функцией Drop:
ln[1]:=Drop[{101,203,401,602,332,412},3]
Out[1]={602,332,412}


| Если количество удаляемых элементов больше длины списка, то выбрасывается ошибка. Если равно длине списка, то возращается пустой список {}


Справочник

{2,3,4}+{5,6,2}	арифметические операции
Sort[{5,7,1}]	сортировка списка
Length[{3,3}]	длина списка (количество элементов)
Total[{1,1,2}]	сумма элементов списка
Count[{3,2,3},3]	количество вхождений элемента в список
First[{2,3}]	первый элемент списка
Last[{6,7,8}]	последний элемент списка
Part[{3,1,4},2]	элемент списка на указанной позиции
Take[{6,4,3,1},2]	создание списка из первых элементов
Drop[{6,4,3,1},2]	удаление первых элементов в списке
IntegerDigits[1234]	список цифр данного целого числа

Упражнения
| Ответы к упражнениям здесь

5.1 Создайте список из первых десяти квадратов натуральных чисел, записанных в обратном порядке.

5.2 Найдите сумму первых десяти квадратов натуральных чисел.

5.3 Постройте график первых десяти квадратов целых чисел, начиная с 1.

5.4 С помощью функций Sort, Join и Range создайте список {1, 1, 2, 2, 3, 3, 4, 4}.

5.5 C помощью функции Range и + создайте список целых чисел от 10 до 20 включительно.

5.6 Сформируйте список, состоящий из квадратов и кубов пяти первых натуральных чисел, упорядоченных по возрастанию.

5.7 Найдите количество цифр числа 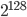$2^{128}$.

5.8 Найдите первую цифру числа 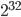$2^{32}$.

5.9 Найдите первые десять цифр числа 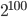$2^{100}$.

5.10 Найдите наибольшую цифру числа 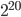$2^{20}$.

5.11 Найдите количество нулей в записи числа 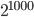$2^{1000}$

5.12 С помощью функций Part, Sort и IntegerDigits определите наименьшую цифру числа, получающегося из числа 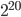$2^{20}$ удалением наименьшей цифры.

5.13 Постройте график последовательности цифр числа 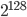$2^{128}$ | (то есть ось абсцисс соответствует номеру цифры, а ось ординат - самой цифре).

5.14 Используя функции Take и Drop список целых чисел от 11 до 20 включительно из списка Range[100].

x5.1 Создайте список первых десяти натуральных чисел, увеличенных в 3 раза.

x5.2Используя только функции Range и Times сформируйте список квадратов первх десяти натуральных чисел.

х5.3 Найдите последнюю цифру числа 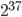$2^{37}$

x5.4 Найдите препоследнюю цифру числа 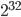$2^{32}$

x5.5 Найдите сумму цифр числа 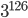$3^{126}$

x5.6 Постройте круговую диаграмму количества вхождений цифр в число 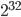$2^{32}$

x5.7 Создайте списко круговых диаграмм количества вхождений цифр в числа 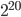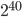$2^{20}$, $2^{40}$ и $2^{60}$.

Ответы к упражнениям

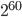5.2 385

5.7 39

5.8 4

5.10 8

5.11 28

5.12 1

x5.3 2

x5.4 9

x5.5 234

Вопросы и ответы

Можно ли складывать списки разной длины?

Нет. {1, 2} + {1, 2, 3} не будет работать,в отличие от {1, 2, 0}+{1, 2, 3}.

Может ли список не содержать ни одного элемента?

Да. Длина списка {} равна 0, в нем нет элементов. Такой список обычно называют нулевым (null list) или пустым списком.

Примечания

• Функция IntegerDigits[5671] возвращает цифры в десятичной системе счисления. Функция IntegerDigits[5671, 2] - в двоичной. Вы можете выбрать любое основание, какое захотите. Функция FromDigits[{5,6,7,1}] формирует число из цифр переданного списка.
• Функция Rest[список] возвращает список без первого элемента. Функция Most[список] возвращает список без последнего элемента.

предыдущая глава           следующая глава

Перевод с дополнениями: И.Колемаев

источник http://www.wolfram.com/language/elementary-introduction/05-operations-on-lists.html

перейти к содержанию