Задачи из книги "Олимпиадные задачи по программированию"
Ф. Меньшиков

Четвертая тренировка

содержание задачника

Задача 4А. Совершенные числа

Число называется совершенным, если оно равно сумме всех своих делителей, меньших его самого. Требуется найти все совершенные числа от М до N.
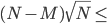Ограничения: М и N целые, 1 $\le$M$\le$N$\le$ 10⁹, $(N-M)\sqrt{N}\le$ 10⁷, время 5 с.
Ввод из файла perfect.in. В первой строке находятся разделенные пробелом числа M и N.
Вывод в файл perfect.out. В каждой строке вывести по одному числу в порядке возрастания. Если совершенных чисел в промежутке нет, вывести Absent.
Примеры
Ввод
6 6
Вывод
6
Ввод
4 5
Вывод
Absent

Задача 4B. Разложение на слагаемые

Вывести все представления натурального числа N суммой натуральных чисел.
Перестановка слагаемых нового способа представления не дает.
Ограничения: 2 $\le$ N$\le$ 40, время 2 с.
Ввод из файла decomp.in. В первой строке находится единственное число N.
Вывод в файл decomp.out. В каждой строке выводится одно из представлений.
В сумме слагаемые разделяются знаком «+».
Пример
Ввод
4
Вывод
1+1+1+1
1+2+1
1+3
2+2

Задача 4С. Гангстеры

N гангстеров собираются в ресторан, i-й гангстер приходит в момент времени T_i, богатство этого гангстера — P_i. Дверь ресторана имеет К + 1 степень открытости, они обозначаются целыми числами из интервала [0, К]. Степень открытости двери может изменяться на единицу в единицу времени, то есть дверь может открыться на единицу, закрыться на единицу или остаться в том же положении, в котором была. В начальный момент времени дверь закрыта (положение 0). i-й гангстер заходит в ресторан, только если дверь открыта специально для него, то есть когда степень открытости двери соответствует его полноте S_i. Если в момент, когда гангстер подходит к ресторану, степень открытости двери не соответствует его полноте, он уходит и больше не возвращается. Ресторан работает в интервале времени [0, Т]. Требуется собрать гангстеров с максимальным суммарным богатством в ресторане, открывая и закрывая дверь соответствующим образом.
Ограничения: 1 $\le$ N$\le$100, 1 $\le$K$\le$ 100, 1 $\le$ T$\le$ 30 000, 0 $\le$Т_i $\le$ T, 1 $\le$ Р_i $\le$ 300, 1 $\le$ S_i $\le$ К, все числа целые, время 2 с.
Ввод из файла gangster.in. В первой строке находятся числа N, К, Т, во второй — Т₁,Т₂,..., T_N, в третьей — Р₁, Р₂,..., P_N, в четвертой — S₁, S₂,..., S_N. Числа в строках разделены пробелами.
Вывод в файл gangster.out. Вывести одно число — максимальное суммарное богатство гангстеров, попавших в ресторан. Если зайти не удалось никому, вывести 0.
Примеры
Ввод
4 10 20
10 16 8 16
10 11 15 1
10 7 1 8
Вывод
26
Ввод
2 17 100
5 0
50 33
6 1
Вывод
0

Задача 4D. Площадь многоугольника

Многоугольник на плоскости задан целочисленными координатами своих N вершин в декартовой системе координат. Требуется найти площадь многоугольника.
Стороны многоугольника не соприкасаются (за исключением соседних — в вершинах) и не пересекаются.
Ограничения: 3 $\le$ N$\le$ 50 000, координаты вершин целые и по модулю не превосходят 20 000, время 1 с.
Ввод из файла area.in. В первой строке находится число N. В следующих N строках находятся пары чисел — координаты точек. Если соединить точки в данном порядке, а также первую и последнюю точки, получится заданный многоугольник.
Вывод в файл area.out. Вывести одно число — площадь многоугольника. Его следует округлить до ближайшего числа с одной цифрой после запятой.
Примеры
Ввод
4
5 0
0 5
-5 0
0 -5
Вывод
50.0
Ввод
4
0 4
0 0
3 0
1 1
Вывод
3.5

Задача 4E. Деление длинного числа на короткое

Даны целое неотрицательное число М и целое положительное число N. Найти M div N и M mod N (частное и остаток от целочисленного деления M на N).
Ограничения: 0 $\le$M$\le$10⁶⁰⁰⁰⁰, 1 $\le$ N$\le$ 1 000 000, время 1 с.
Ввод из файла divshdrt.in. В первой строке находитсячисло М, во второй — N.
Вывод в файл divshort.out. В первой строке вывести значение выражения M div N, во второй — выражения M mod N.
Пример
Ввод
12345678901234567890
1000
Вывод
12345678901234567
890

Задача 4F. Скобки

Дана последовательность из N круглых, квадратных и фигурных скобок. Выяснить, можно ли добавить в нее цифры и знаки арифметических действий так, чтобы получилось правильное арифметическое выражение.
Ограничения: 1 $\le$ N$\le$ 100 000, время 1 с.
Ввод из файла bracket.in. В первой строке находится число скобок N, во второй —N символов из набора (, ), [, ], {,}.
Вывод в файл bracket.out. Выводится слово Yes, если получить правильное арифметическое выражение можно, или No, если нельзя.
Примеры
Ввод
6
([())]
Вывод
No
Ввод
24
{[()([]{})[]]({}{{}})}[]
Вывод
Yes

содержание задачника