Условия задач олимпиады по математике МФТИ 2017

Билет 1

1. Когда к квадратному трехчлену 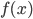$f(x)$ прибавили 2, его наименьшее значение увеличилось на 1, а когда из него вычли 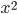$x^2$, его наименьшее значение уменьшилось на 3. А как изменится наименьшее значение 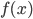$f(x)$, если к нему прибавить $2x^2$?
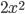2. Решите неравенство $x^{\log_3x}-2\le(\sqrt[3]{3})^{\log_{\sqrt{3}}^2x}-2x^{\log_3\sqrt[3]{x}}$
3. Известно, что числа 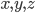$x,y,z$ образуют в указанном порядке арифметическую прогрессию с разностью 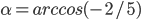$\alpha=arccos(-2/5)$, а числа 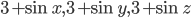$3+\sin x,3+\sin y,3+\sin z$ образуют в указанном порядке непостоянную геометрическую прогрессию. Найдите $\sin y$.
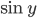4. В треугольнике ABC угол при вершине A в два раза больше угла при вершине C. Через вершину B проведена касательная ℓ к окружности Ω, описанной около треугольника ABC.
   Расстояния от точек A и C до этой касательной равны соответственно 4 и 9.
   а) Найдите расстояние от точки A до прямой BC.
   б) Найдите радиус окружности Ω и длину стороны AB.
5. На координатной плоскости рассматриваются квадраты, все вершины которых имеют целые неотрицательные координаты, а центр находится в точке (60;45). Найдите количество таких квадратов.
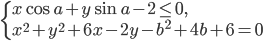6. Найдите все значения параметра $b$ такие, что система $\left\{\begin{array}{l l} x\cos a+y\sin a-2\le0,\\ x^2+y^2+6x-2y-b^2+4b+6=0 \end{array}\right.$  имеет хотя бы одно решение при любом значении параметра $a$.
7. Основание треугольной пирамиды ABCD - правильный треугольник ABC. Объем пирамиды равен 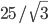$25/\sqrt{3}$, а ее высота, проведенная из вершины D, равна 3. Точка M - середина ребра CD. Известно, что радиусы сфер, вписанных в пирамиды ABCM и ABDM, равны между собой. а) Найдите все возможные значения угла между гранями пирамиды при ребре AB; б) Найдите все возможные значения длины ребра CD, если дополнительно известно, что грани BCD и ABC взаимно перпендикулярны.

Варианты вступительных экзаменов