Вступительное испытание
по математике в МГУ 2015 года
- Найдите
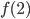 , если
, если 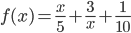 .
.
Ответ: 2 - Найдите сумму квадратов корней уравнения
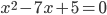 .
.
Ответ: 39 - Решите неравенство
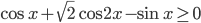 .
.
Ответ:![x\in [-5\pi/12+2n\pi;\pi/4+2n\pi]\cup [11\pi/12+2n\pi; 5\pi/4+2n\pi], n\in Z](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4436061dcd4feac2a2002dcb2f7fe67d.gif)
- Решите уравнение
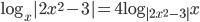 Ответ:
Ответ: 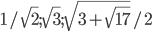
- Окружность радиуса 3/2 касается середины стороны BC треугольника ABC и пересекает сторону AB в точках D и E, так что AD : DE : EB = 1 : 2 : 1. Чему может равняться АС, если угол ВАС равен 30о?
Ответ: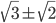
- Велосипедист Василий выехал из А в Б. Проехав треть пути, Василий наткнулся на выбоину, вследствие чего велосипед безнадежно вышел из строя. Не теряя времени, Василий бросил сломавшийся велосипед и пошел пешком обратно в А за новым велосипедом. В момент поломки из А выехал мотоциклист Григорий. На каком расстоянии от А он встретит Василия, если пункт Б отстоит от А на 4 км, а Василий доберется до А тогда же, когда Григорий до Б? Скорости велосипеда, мотоцикла и пешехода считать постоянными.
Ответ: 1 км - В правильную треугольную призму с основаниями ABC, A1B1C1 и ребрами AA1, BB1, CC1 вписана сфера. Найдите ее радиус, если известно, что расстояние между прямыми AE и BD равно
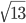 . где E и D - точки, лежащие на A1B1 и B1C1 соответственно, и A1E : EB1 = B1D : DC1 = 1 : 2.
. где E и D - точки, лежащие на A1B1 и B1C1 соответственно, и A1E : EB1 = B1D : DC1 = 1 : 2.
Ответ: 13/6 - Найдите все пары
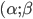 , при которых достигается максимум выражения
, при которых достигается максимум выражения 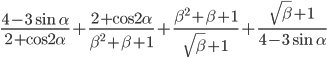
Ответ: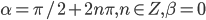
смотрите еще МГУ. Дополнительное вступительное испытание 2013
