Вступительное испытание
по математике в МГУ 2016 года

Июль 2016 г

1. Сколько различных решений имеет уравнение $2x\sqrt{11}-\sqrt[4]{77}(2-x^2)=2x\sqrt{7}+3(x^2+2)$
2. Решите неравенство $\displaystyle\frac{2x}{5x+3}\le\frac{x-2}{3x-7}$
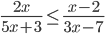
3. Решите уравнение $\sin 4x-3\sin 3x-2\sin 2x-3\sin x=0$
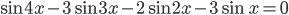
4. В геометрической прогрессии разность одиннадцатого и пятого членов (в указанном порядке) в 21 раз больше, чем разность седьмого и пятого членов (в указанном порядке). Сумма восьми первых членов этой прогрессии равна 1020. Чему равен четвертый член этой прогрессии?
5. Решите систему уравнений $\left\{\begin{array}{l l}5^y=25x,\\2\log_5x-3\log_x5=y\end{array}\right.$
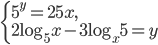
6. Дана трапеция с основаниями длины 1 и 7. Одна окружность вписана в эту трапецию, а другая окружность описана около этой трапеции. Найдите радиус описанной окружности.
7. Решите уравнение $\sqrt{x^2-x-6}=\sqrt{x^2+4x-5}+\sqrt{2x^2+3x-11}$.
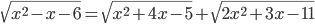8. В правильной треугольной пирамиде SABC высота в 2 раза больше, чем сторона основания. На боковых ребрах SA, SB и SC выбраны точки M, N и K соответственно так, что SM:MA = 5:1, SN:NB = 1:2, SK:KC = 1:2. Найдите угол между плоскостью, проходящей через точки M, N, K, и плоскостью основания пирамиды.

смотрите еще Вступительные экзамены и МГУ. Дополнительное вступительное испытание 2013