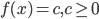Функциональные уравнения
- Существует ли линейная функция
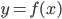 , удовлетворяющая при всех
, удовлетворяющая при всех  соотношению
соотношению 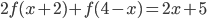 ?
? - Найдите квадратичную функцию
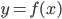 , удовлетворяющую при всех
, удовлетворяющую при всех  уравнению
уравнению 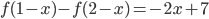 .
. - Существует ли квадратичная функция
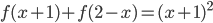 ?
? - Найдите все многочлены степени n, удовлетворяющие тождеству
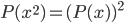 при
при 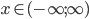 .
. - Найдите функцию
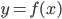 , удовлетворяющую при всех
, удовлетворяющую при всех 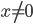 соотношению
соотношению 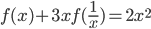 .
. - Найдите значения
 , при которых функция
, при которых функция 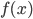 , удовлетворяющая при всех
, удовлетворяющая при всех 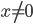 и
и 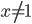 уравнению
уравнению 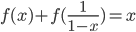 , имеет экстремумы. Найдите эту функцию.
, имеет экстремумы. Найдите эту функцию. - Задана функция
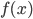 , причем
, причем 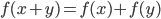 для всех рациональных чисел
для всех рациональных чисел  и
и 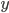 . Найдите
. Найдите 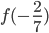 , если
, если 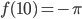 .
. - Задана функция
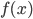 , причем
, причем 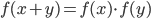 для всех рациональных чисел
для всех рациональных чисел  и
и 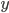 . Известно, что
. Известно, что 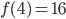 . Найдите
. Найдите 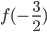 .
. - Функция для любых действительных значений
 и
и 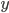 удовлетворяет равенству
удовлетворяет равенству 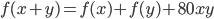 . Найдите
. Найдите 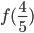 , если
, если 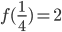 .
. - Функция
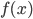 при каждом действительном
при каждом действительном  удовлетворяет равенству
удовлетворяет равенству 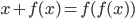 . Решите уравнение
. Решите уравнение 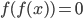 .
. - Найдите все функции
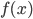 , определенные на всей числовой прямой, для которых неравенство
, определенные на всей числовой прямой, для которых неравенство 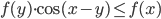 выполнено при любых
выполнено при любых  и
и 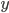 .
.
Ответы
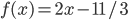
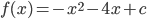 , c - произвольная константа
, c - произвольная константа- нет
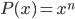
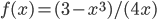
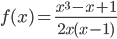
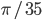
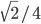
- 24
- 0