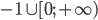Показательные неравенства
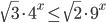
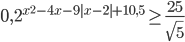
- Решите неравенство
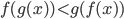 , где
, где 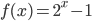 и
и 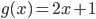
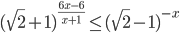
![\sqrt[3]{2}^{x^2+4x+1}-(\sqrt{3+\sqrt{8}}-1)^x\leq 0](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_fb601d041fcd140039e231d673702a9f.gif)
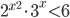
- Число
 подобрано так, что меньший корень уравнения
подобрано так, что меньший корень уравнения 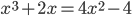 является одновременно одним из решений неравенства
является одновременно одним из решений неравенства 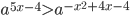 . Решите это неравенство.
. Решите это неравенство. 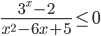
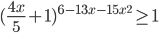
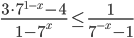
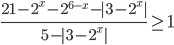
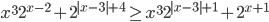
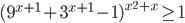
Ответы
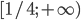
- [-6; 1]U[3; 10]
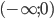
![(-1;2]\cup [3;+\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_04c9e057d2b3951481524813edb5fb00.gif)
- [-2; -1/2]
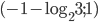
- (-1; 0)
![(-\infty; \log_32]\cup (1;5)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b6081dbbbe0175626e8509eb471d0ff7.gif)
![(-5/4; -6/5]\cup [0;1/3]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_765b4778f24dc91cc1585c0018171b01.gif)
![(0;\log_73]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_980293123427717b442918a724ec78e0.gif)
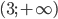
![(-\infty;2]\cup[3;+\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c9f93b0df5a3451a00e423fee9da3601.gif)
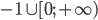
Показательные неравенства
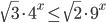
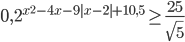
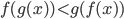 , где
, где 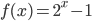 и
и 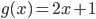
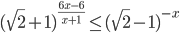
![\sqrt[3]{2}^{x^2+4x+1}-(\sqrt{3+\sqrt{8}}-1)^x\leq 0](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_fb601d041fcd140039e231d673702a9f.gif)
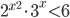
 подобрано так, что меньший корень уравнения
подобрано так, что меньший корень уравнения 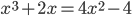 является одновременно одним из решений неравенства
является одновременно одним из решений неравенства 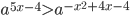 . Решите это неравенство.
. Решите это неравенство.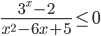
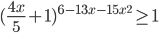
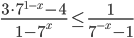
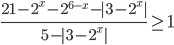
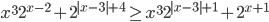
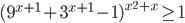
Ответы
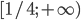
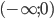
![(-1;2]\cup [3;+\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_04c9e057d2b3951481524813edb5fb00.gif)
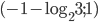
![(-\infty; \log_32]\cup (1;5)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b6081dbbbe0175626e8509eb471d0ff7.gif)
![(-5/4; -6/5]\cup [0;1/3]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_765b4778f24dc91cc1585c0018171b01.gif)
![(0;\log_73]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_980293123427717b442918a724ec78e0.gif)
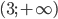
![(-\infty;2]\cup[3;+\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c9f93b0df5a3451a00e423fee9da3601.gif)