Олимпиадная математика. Четырнадцатая серия задач

Олимпиадные задачи по математике. Подборка задач для школьников

В треугольнике АВС проведены медиана ВМ и высота СН. Найдите АС, если МН = 10.
Дан квадрат ABCD. На сторонах ВС и CD выбраны точки К и N так, что BK =KC, CN : ND = 2 : 1. Отрезки AK и BN пересекаются в точке Т. Найдите площадь треугольника BTA, если площадь четырехугольника KCNT равна 13.
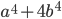Найдите все целые $a$ и $b$ такие, что число $a^4+4b^4$ является простым.
Докажите, что 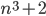$n^3+2$ не делится на 9 ни при каких натуральных $n$
В некоторой стране 15 городов, каждый из которых соединен дорогами не менее чем с 7 другими. Верно ли, что из любого города можно добраться до любого другого (возможно, проезжая через другие города)?
На доске было записано арифметическое выражение, значение которого равно 2007. Вася поменял в этом выражении два знака действия местами, и значение выражения стало равным 2008. Приведите пример такого выражения.
Назовем число вида 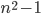$n^2-1$ почти квадратом натурального числа $n$ . Докажите, что произведение двух почти квадратов натуральных чисел всегда равно разности каких-то двух квадратов натуральных чисел.
Каждая из точек плоскости покрашена в один из трех цветов, причем все три цвета используются. Верно ли, что при любой такой покраске можно выбрать окружность, на которой есть точки всех трех цветов?
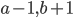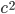Набор, который состоит из целых чисел a, b и с, заменили на набор из чисел $a-1, b+1$ и $c^2$ . В результате получившийся набор совпал с исходным. Найдите числа 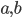$a, b$ и $c$ , если их сумма равна 2005.
По кругу висят 250 лампочек. Все лампочки включены. Разрешается либо переключить любые 4 последовательные лампочки, либо 5 последовательных лампочек кроме средней. Можно ли выключить все лампочки?