Олимпиадные задачи по математике. Подборка задач для школьников
-
Однажды в газете напечатали такое сообщение из-за рубежа: «Министр социального обеспечения Великобритании Николас Скотт сообщил депутатам парламента, что с 1984 по 1988 год число мужчин, достигших столетнего возраста, увеличилось в стране со 100 до 210. В случае сохранения этой тенденции через 66 лет на Британских островах почти невозможно будет встретить мужчину моложе 100 лет». Каким образом министр получил число 66 и как вы относитесь к его выводу?
-
Натуральное число
 является произведением двух различных простых чисел, а сумма всех его делителей, считая 1, но не считая
является произведением двух различных простых чисел, а сумма всех его делителей, считая 1, но не считая  , равна 1000. Найдите все такие
, равна 1000. Найдите все такие 
-
На стороне BC равнобедренного треугольника АВС (АВ = ВС) взяли точки N и M (N ближе к В, чем М), такие, что NM = AM и угол МАС равен углу BAN. Найдите угол CAN
-
Докажите, что при любых отличных от нуля числах
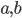 и
и  хотя бы одно из квадратных уравнений
хотя бы одно из квадратных уравнений 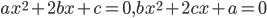 и
и 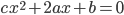 имеет корень.
имеет корень. -
Каждую грань кубика разбили на четыре одинаковых квадрата, а затем раскрасили эти квадраты в несколько цветов так, что квадраты, имеющие общую сторону, оказались окрашенными в различные цвета. Какое наибольшее количество квадратов одного цвета могло получиться?
-
На главной диагонали шашечной доски 10 х 10 стоит десять шашек (все в разных клетках). За один ход разрешается выбрать любую пару шашек и передвинуть каждую из них на одну клетку вниз. Можно ли за несколько таких ходов поставить все шашки на нижнюю горизонталь?
-
Найдите все целые
 , при которых уравнение
, при которых уравнение 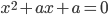 имеет целый корень.
имеет целый корень. -
В окружности проведены две пересекающиеся хорды АВ и CD. На отрезке АВ взяли точку М так, что АМ = АС,а на отрезке CD - точку N так, что DN = DB. Докажите, что если точки M и N не совпадают, то прямая MN параллельна прямой AD.
-
На полке в произвольном порядке стоит десятитомное собрание сочинений Ильфа и Петрова. Библиотекарь может взять любой том с полки и поставить его на пятое место (считая слева). Докажите, что с помощью нескольких таких операций библиотекарь сможет расставить тома в порядке возрастания номеров.
- Существуют ли такие двузначные числа
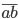 и
и 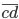 , что
, что 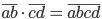 ?
?