Олимпиадные задачи по математике. Подборка задач для школьников
-
Найдите сумму всех четных натуральных чисел, не превосходящих 1000 и не кратных 5.
-
На клетчатой бумаге отмечены 100 вершин соседних клеток, расположенных в одном ряду клеток (то есть получилось два ряда из 50 точек каждый). Найдите число равнобедренных треугольников с вершинами в отмеченных точек.
- Про действительное число
 высказаны следующие утверждения: 1)
высказаны следующие утверждения: 1)  - целое число; 2)
- целое число; 2) 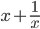 - целое число; 3)
- целое число; 3) 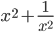 - целое число; 4)
- целое число; 4) 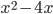 - целое число. Известно, что из этих утверждений ровно три верны. Найдите все такие
- целое число. Известно, что из этих утверждений ровно три верны. Найдите все такие 
- Найдите все значения
 , при которых квадратное уравнение
, при которых квадратное уравнение 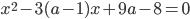 имеет такие корни
имеет такие корни 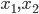 , а уравнение
, а уравнение 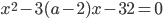 - такие корни
- такие корни 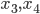 , что числа
, что числа 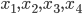 образуют геометрическую прогрессию.
образуют геометрическую прогрессию. - Шары одинакового радиуса расположили один раз в форме правильного треугольника, а другой - в форме прямоугольника. Найдите количество шаров, если и на стороне треугольника, и на большей стороне прямоугольника располагается на 2 шара больше, чем на меньшей стороне прямоугольника.
- Пусть
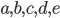 - действительные числа такие, что
- действительные числа такие, что 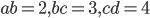 и
и 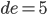 . Найдите
. Найдите 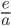
- Два квадрата со стороной 1 имеют общую вершину, и сторона одного квадрата лежит на диагонали второго. Найдите площадь общей части квадратов.
- Поезд состоит из пяти пронумерованных вагонов, расположенных за локомотивом. Сколько существует различных способов соединить вагоны так, чтобы первый вагон был ближе к локомотиву, чем второй вагон?
- Числа 1, 2 и 3 записали по кругу. Затем между каждыми двумя соседними числами записали их сумму. Получилось шесть чисел (1, 3, 2, 5, 3, 4), записанных по кругу. Эту операцию повторили еще четыре раза. В результате получилось 96 чисел. Чему равна их сумма?
- Петя вычеркнул одно из десяти последовательных натуральных чисел. Сумма оставшихся чисел оказалась равна 2006. Какое число вычеркнул Петя?