Олимпиадная математика. Тринадцатая серия задач

Олимпиадные задачи по математике. Подборка задач для школьников

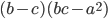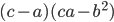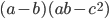Могут ли числа $(b-c)(bc-a^2)$ , $(c-a)(ca-b^2)$ и $(a-b)(ab-c^2)$ быть положительными одновременно?
В треугольнике ABC на сторонах АВ и ВС соответственно отмечены точки D и E так, что AD:BD=BE:EC=2 и угол ACB в два раза больше угла BED. Докажите, что треугольник АВС равнобедренный.
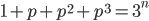
Решите уравнение в целых числах $1+p+p^2+p^3=3^n$
На окружности расположены 1999 белых точек и одна красная точка. Рассмотрим все выпуклые многоугольники с вершинами в этих точках. Каких многоугольников больше: тех, у которых есть красная вершина, или тех, у которых ее нет?
Найдите 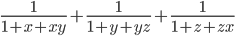$\frac{1}{1+x+xy}+\frac{1}{1+y+yz}+\frac{1}{1+z+zx}$ , если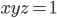 $xyz=1$
Найдите все такие двузначные числа x, для каждого из которых истинны ровно три из следующих шести утверждений: 1) x делится на 3; 2) x делится на 5; 3) х делится на 9; 4) х делится на 15; 5) х делится на 25; 6) х делится на 45.
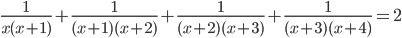
Решите уравнение $\frac{1}{x(x+1)}+\frac{1}{(x+1)(x+2)}+\frac{1}{(x+2)(x+3)}+\frac{1}{(x+3)(x+4)}=2$
В школьной олимпиаде по математике участвовало 100 человек, по физике - 50 человек, по информатике - 48. Когда каждого из учеников спросили, в скольких олимпиадах он участвовал, ответ "по крайней мере в двух" дали в два раза меньше, чем ответ "не менее чем в одной", а ответ "в трех" - втрое меньше человек, чем ответ "не менее чем в одной". Сколько всего учеников приняло участие в этих олимпиадах?
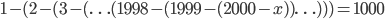
Решите уравнение $1-(2-(3-(\ldots (1998-(1999-(2000-x))\ldots )))=1000$
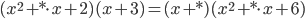Вместо знаков $*$ вставьте такие числа, чтобы равенство $(x^2+*\cdot x+2)(x+3)=(x+*)(x^2+*\cdot x+6)$ стало тождеством.