- Докажите, что квадратное уравнение 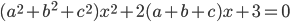$$(a^2+b^2+c^2)x^2+2(a+b+c)x+3=0$$ имеет корни только при $$a=b=c$$.
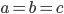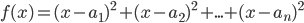- Найдите, при каком значении $$x$$ функция $$f(x)=(x-a_1)^2+(x-a_2)^2+…+(x-a_n)^2$$ принимает наименьшее значение.
- Докажите, что квадратное уравнение 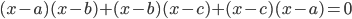$$(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0$$ имеет хотя бы один корень.
- Найдите сумму корней всех квадратных трехчленов вида 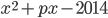$$x^2+px-2014$$, где $$p$$ принимает целые значения от -100 до 100 включительно.
- Докажите, что графики квадратичных функций 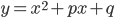$$y=x^2+px+q$$, у которых 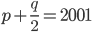$$p+\frac{q}{2}=2001$$, проходят через одну точку.
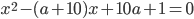- При каких значениях параметра $$a$$ корни уравнения $$x^2-(a+10)x+10a+1=0$$ являются целыми числами?
- Корни квадратного уравнения 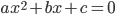$$ax^2+bx+c=0$$ в 2007 раз больше корней квадратного уравнения 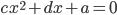$$cx^2+dx+a=0$$. Докажите, что $$b^2=d^2$$.
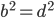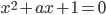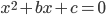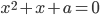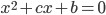- Различные числа $$a$$, $$b$$ и $$c$$ таковы, что уравнения $$x^2+ax+1=0$$ и $$x^2+bx+c=0$$ имеют общий корень. Кроме того, общий корень имеют уравнения $$x^2+x+a=0$$ и $$x^2+cx+b=0$$. Найдите сумму $$a+b+c$$.
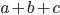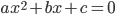- Докажите, что если коэффициенты $$a$$, $$b$$ и $$c$$ уравнения $$ax^2+bx+c=0$$ связаны условием 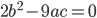$$2b^2-9ac=0$$, то отношение корней уравнения равно 2.
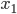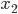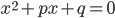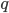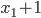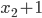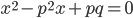- Пусть $$x_1$$ и $$x_2$$ – корни уравнения $$x^2+px+q=0$$. Найдите $$p$$ и $$q$$, если известно, что $$x_1+1$$ и $$x_2+1$$ являются корнями уравнения $$x^2-p^2x+pq=0$$.