- Доказать, что среди любых n+1 натуральных чисел найдутся два числа, которые при делении на n дают одинаковые остатки.
- Доказать, что среди любых n+1 натуральных чисел найдутся два числа таких, что их разность делится на n.
- Доказать, что из любых трех целых чисел можно найти два, сумма которых четна.
- Доказать, что из совокупности любых
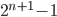целых чисел можно найти 
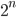чисел, сумма которых делится на 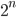. - Даны 12 различных двузначных натуральных чисел. Доказать, что из них можно выбрать 2 числа, разность которых – двузначное число, записываемое двумя одинаковыми цифрами.
- Доказать, что найдется число вида 11…10…00, делящееся на 1998.
- Доказать, что среди чисел, записываемых только единицами, есть число, которое делится на 1997.
- Доказать, что существует натуральное число, последние цифры которого 1996 и которое делится на 1997.
- Можно ли найти такие два (различные) степени числа 4, у которых а) последняя цифра одинакова? б) две последние цифры одинаковы? в) три последние цифры одинаковы?
- Можно ли найти такую натуральную степень числа 3, которая оканчивается на …0001?
- Верно ли, что среди любых семи натуральных чисел найдутся три, сумма которых делится на 3?
- Имеются n целых чисел. Доказать, что среди них всегда найдутся несколько (или, может быть, одно), сумма которых делится на n, если а) n = 3; б) n = 100; в) n – любое.
- Докажите, что есть целые числа m и n взаимно просты, то найдется такое натуральное k, что делится на n.
- Докажите, что среди любых 9 последовательных натуральных чисел найдется по крайней мере одно, взаимно простое с каждым из остальных.
- Сумма 100 натуральных чисел, каждое из которых не больше 100, равно 200. Доказать, что из них можно выбрать несколько чисел, сумма которых равна 100.
- Докажите, что среди любых 39 последовательных натуральных чисел найдется такое, сумма цифр которого делится на 11.