Подготовка к ЕГЭ. Иррациональные уравнения II
- Решите уравнение
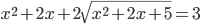
- Найдите сумму корней уравнения
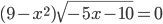
- Решите уравнение
![\sqrt{x+4}-\sqrt[3]{x+1}=1](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_be182afca938a0656519632fbd16cfee.gif)
- Найдите сумму абсцисс точек пересечения графиков функций
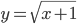 и
и ![y=\sqrt[3]{2x+1}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_102bfe2ee34741a7735b893c28914631.gif)
- При каких значениях
 сумма значений функций
сумма значений функций 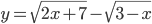 и
и 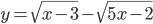 равна 0?
равна 0? - Решите уравнение
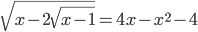
- Определите количество корней уравнения
![\sqrt[4]{(x-4)^4}=4-x^2](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_ec606726c1ec6fe446dd7c9e19312f00.gif)
- Найдите корни уравнения
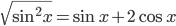
- Решите уравнение
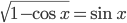
- Найдите количество корней уравнения
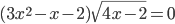
- Найдите все
 , для которых выполняется равенство
, для которых выполняется равенство 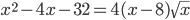
- Найдите абсциссы точек пересечения графиков функций
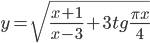 и
и 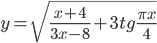 .
. - Найдите наибольший корень уравнения
![3\sqrt{-x^2+9x-14}-9\sqrt[8]{x^2-5x-14}-1=\cos \pi x](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a7e8f1a061dc4c09d4a9a3f66adc5966.gif)
- Найдите корни уравнения
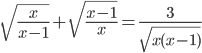
- При каких значениях
 значение функции
значение функции 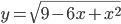 не больше и не меньше значения функции
не больше и не меньше значения функции 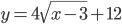 ?
? - При каких
 высказывание
высказывание 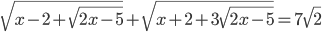 обращается в истинное?
обращается в истинное?
Ответы
- -1
- -5
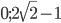
- 1
- 3
- 2
- 2
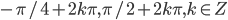
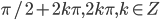
- 2
- 4;8
- 1
- 7
- -1;2
- 39
- 15