Подготовка к ЕГЭ. Преобразование иррациональных выражений
- Найдите значение выражения
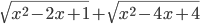 , если
, если 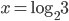
- Найдите значение выражения
![\sqrt[4]{(x^2-6x+9)^2}+\sqrt[4]{(x^2+6x+9)^2}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_922371319f42054548fbe105a5b99ef1.gif) , если
, если 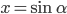
- При
![x=\sqrt[3]{3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_820d6d48a4f8857c0c5d5b9a7334161e.gif) найдите значение выражения
найдите значение выражения ![\sqrt{x^2+2x+1}+2\sqrt[4]{(x^2-4x+4)^2}+\sqrt[6]{(x^2-2x+1)^3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_920afcdd93cb491cbb963ab07775e730.gif)
- При
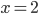 найдите значение выражения
найдите значение выражения ![\sqrt[4]{(2\sqrt{x}-5)^4}+\sqrt[3]{(2\sqrt{x}-3)^3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_83614833790048b3cc44828d2a3547db.gif)
- При
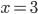 найдите значение выражения
найдите значение выражения 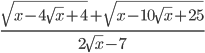
- Упростите
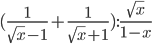
- Найдите значение выражения
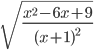 , если
, если 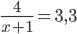
- При
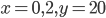 найдите значение выражения
найдите значение выражения 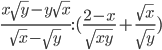
- Найдите
![\sqrt[10]{(x-2\frac{1}{5})^{10}}+\sqrt[10]{(x-2,8)^{10}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c2e0bed5aee3ace2eb6249abea475c9e.gif) , если
, если 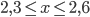
- При
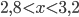 вычислите
вычислите ![|x-3,5|+\sqrt[4]{(9+6x+x^2)^2}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_14a1d159e0a46c6a45605c4400ac0211.gif)
- При
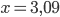 вычислите
вычислите 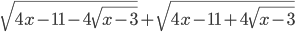
- Вычислите
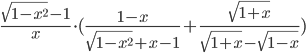 , если
, если 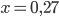
- График функции
![y=\displaystyle\frac{\sqrt[6]{(x\sqrt{2}-3)^6}}{\sqrt[3]{(x\sqrt{32}-12)^3}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_13c04a7e17b0ea7707c78160fe313824.gif) пересекается с графиком функции
пересекается с графиком функции 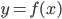 в точке
в точке 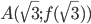 . Найдите
. Найдите 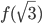
- Найдите значение выражения
![2-\sqrt[6]{(x-1)^2(x+4)^4}\cdot\sqrt[6]{(x+4)^2(x-1)^4}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_06ee52f9b1156e67833e22360018daa0.gif) , если
, если 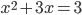
- Упростите
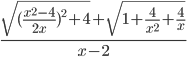 , если
, если 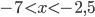
- Упростите
![\displaystyle\frac{\sqrt[4]{a^5}+\sqrt[4]{ab^4}-\sqrt[4]{a^4b}-\sqrt[4]{b^5}}{a\sqrt{a}-a\sqrt{b}+b\sqrt{a}-b\sqrt{b}}\cdot (\sqrt[4]{a}+\sqrt[4]{b})](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_0c17f69a5cac2b4dcfed99020737d175.gif)
Ответы
- 1
- 6
- 4
- 2
- -1
- -2
- 2,3
- 2
- 0,6
- 6,5
- 2
- -1
- -0,25
- 1
- -0,5
- 1