Подготовка к ЕГЭ. Свойства функции
- Найдите область определения функции
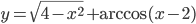
- Найдите все значения
 , которые не принадлежат области определения функции
, которые не принадлежат области определения функции 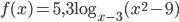
- Найдите наибольшее натуральное
 из области определения функции
из области определения функции ![f(x)=\sqrt[7]{x+2}+\sqrt[4]{x+5}+\lg (6-3x)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_5f794ccd21640e7eb4428fcb6f0be965.gif)
- Найдите область определения функции
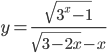
- Найдите множество значений функции
![y=\sqrt[6]{|\cos (3x-2)|}+4](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_56b049897656c0efa39d309e3ca6170e.gif)
- Найдите наибольшее значение функции
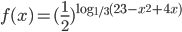
- Найдите сумму наибольшего и наименьшего значений функции
![y=(\sqrt[6]{\frac{16}{\pi}\arccos 93x-2)})^6](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_09819932a7616a10b6730abf2a2c0560.gif)
- Найдите наибольшее целое значение функции
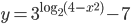
- Найдите область определения функции
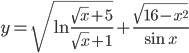
- Найдите количество целых значений
 из области определения функции
из области определения функции 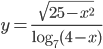
- Укажите наименьшее целое число из области определения функции
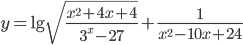
- Укажите количество целых чисел из области определения функции
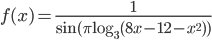
- Найдите множество значений функции
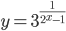
- Укажите наименьшее целое значение функции
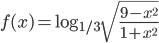
- Найдите сумму наибольшего и наименьшего значений функции
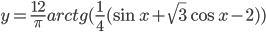
- Сколько целых значений принимает функция
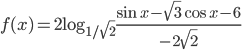 ?
?
Ответы
- [1;2]
![(-\infty; 3]\cup {4}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_96c08a61eeb83fc54b9852c53ab8fe55.gif)
- 1
- [0; 1)U(1; 1,5]
- [4;5]
- 8
- 16
- 2
![(0; \pi)\cup (\pi; 4]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_9ad0664e89e7f05bbcbba39def078645.gif)
- 8
- 5
- 1
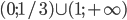
- -1
- -3
- 5