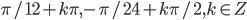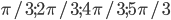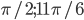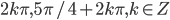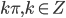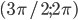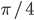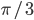Подготовка к ЕГЭ. Тригонометрические уравнения II
- Решите уравнение
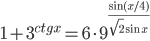
- При каком значении
 значения функции
значения функции 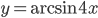 и
и 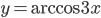 совпадают?
совпадают? - Найдите абсциссы точек пересечения графиков функций
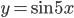 и
и 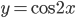
- Найдите наименьший положительный корень уравнения
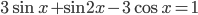
- Найдите сумму корней уравнения
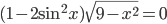
- Найдите наибольший отрицательный корень уравнения
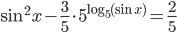
- Определите количество корней уравнения
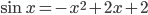
- Решите уравнение
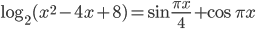
- Найдите все значения
 , при которых выполняется равенство
, при которых выполняется равенство 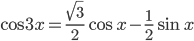
- Найдите все корни уравнения
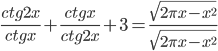
- При каких
 высказывание
высказывание 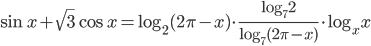 истинное?
истинное? - Решите уравнение
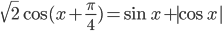
- При каких значениях
 значение функции
значение функции 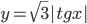 совпадает со значением функции
совпадает со значением функции 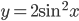 ?
? - Какие числа из промежутка
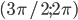 обращают в нуль функцию
обращают в нуль функцию 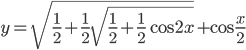 ?
? - Укажите абсциссы точек пересечения графиков функций
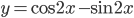 и
и 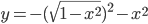 .
. - Найдите наименьший корень уравнения
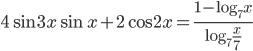
Ответы
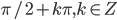
- 0,2
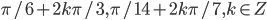
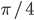
- 0
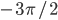
- 2
- 2