Решение диагностической работы по математике
Профильный уровень
10 класс, 2015 г
Условия задач здесь
1. Материал сайта www.itmathrepetitor.ru Всего чисел 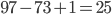 (считаем, что фраза "от 73 до 97" подразумевает отрезок, то есть включая границы). Среди этих чисел ровно 8 делятся на 3.
(считаем, что фраза "от 73 до 97" подразумевает отрезок, то есть включая границы). Среди этих чисел ровно 8 делятся на 3.
Это можно установить прямым подсчетом, так как чисел всего 25. Если бы их было значительно больше, то можно было применить формулы прогрессии, так как числа, делящиеся на 3, образуют арифметическую прогрессию с разностью 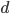 , равной 3.
, равной 3.
Еще полезно знать, что среди  первых натуральных чисел
первых натуральных чисел ![[\displaystyle\frac{n}{k}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_3d5a6bd64f583abea1f7ecb09f04050e.gif) чисел делится на
чисел делится на 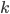 , где
, где ![[x]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_3e5314e9fd31509fdeb83faa0f729ba2.gif) - целая часть числа
- целая часть числа  , то есть наибольшее целое число, не превосходящее
, то есть наибольшее целое число, не превосходящее  .
.
Тогда искомая вероятность равна 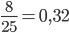 . Дополнительно разобрать задачи с решениями по теории вероятностей можно здесь.
. Дополнительно разобрать задачи с решениями по теории вероятностей можно здесь.
2. Материал сайта www.itmathrepetitor.ru. Так как сумма смежных углов равна 180о, то угол треугольника при основании равен 180-123=57o. В равнобедренном треугольнике углы при основании равны, поэтому второй угол при основании треугольника равен 57o. Так как сумма всех углов треугольника равна 180о, то искомый угол (против основания) равен 180-57-57=66о.
3.1. Движение происходило в течение 5 с. Расстояние в конце 5 с равно 4 м. Тогда средняя скорость движения точки равна 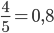 м/c
м/c
3.2. Так как 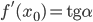 , где
, где  - угол наклона касательной, проведенной к графику функции в точке с абсциссой
- угол наклона касательной, проведенной к графику функции в точке с абсциссой 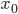 , то рассмотрим треугольник, выделенный красным цветом на рисунке. Так как он прямоугольный с катетами, равными
, то рассмотрим треугольник, выделенный красным цветом на рисунке. Так как он прямоугольный с катетами, равными 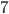 и
и 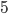 , то
, то 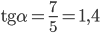 .
.
4. Площадь поверхности равна 10+15+10+5+5+15+7+7=74. Попробуйте самостоятельно определить какая грань какому слагаемому соответствует.
5. Так как 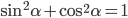 (основное тригонометрическое тождество), то
(основное тригонометрическое тождество), то 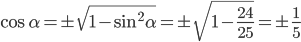 . Обратите внимание на
. Обратите внимание на 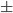 . По условию
. По условию  принадлежит III четверти, поэтому
принадлежит III четверти, поэтому 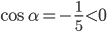 .
.
6. Материал сайта www.itmathrepetitor.ru. Составим уравнение 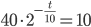 . Тогда
. Тогда 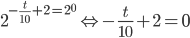 , откуда
, откуда 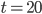 .
.
7. Материал сайта www.itmathrepetitor.ru. Пусть смешали  кг 18-процентного вещества с
кг 18-процентного вещества с  кг 20-процентного этого же вещества. Тогда масса раствора равна
кг 20-процентного этого же вещества. Тогда масса раствора равна 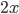 кг. В нем собственно вещества содержится
кг. В нем собственно вещества содержится 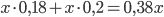 кг. Тогда концентрация в процентах равна
кг. Тогда концентрация в процентах равна 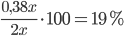 .
.
8. Материал сайта www.itmathrepetitor.ru. Согласно тригонометрических формулам, 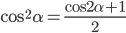 . Поэтому
. Поэтому 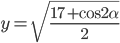 . Так как
. Так как 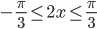 , то
, то 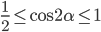 . Значит,
. Значит, 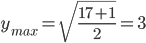 .
.
9. а) Применим к левой части уравнения формулу под номером 42 из справочника тригонометрических формул. Тогда уравнение примет вид 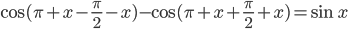 , откуда
, откуда 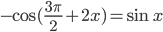 . После применения формул приведения получим, что
. После применения формул приведения получим, что 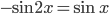
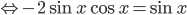 . В последнем переходе пригодилась формула синуса двойного угла.
. В последнем переходе пригодилась формула синуса двойного угла.
Далее самой распространенной ошибкой было бы сократить левую и правую части на 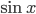 и решить уравнение
и решить уравнение  . Дело в том, что при сокращении происходит потеря корней уравнения
. Дело в том, что при сокращении происходит потеря корней уравнения 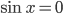 . Поэтому необходимо решить совокупность из двух уравнений:
. Поэтому необходимо решить совокупность из двух уравнений: 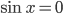 и
и 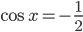 . Получаем
. Получаем 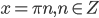 или
или 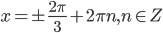
смотрите еще Итоговая работа по математике 10 класс