Решение демонстрационного варианта
контрольных измерительных материалов
единого государственного экзамена 2018 года
по математике
Профильный уровень
 Условия задач и ответы здесь
Условия задач и ответы здесь
13. а) Преобразуем обе части уравнения: 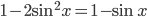

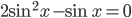

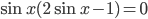 , откуда
, откуда 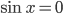 или
или 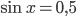 .
.
Из первого уравнения 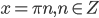 .
.
Из второго уравнения 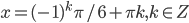 .
.
б) С помощью числовой окружности отберем корни из промежутка 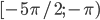 .
. 
Получаем числа 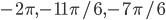 .
.
14. а) Пусть H - середина AC. 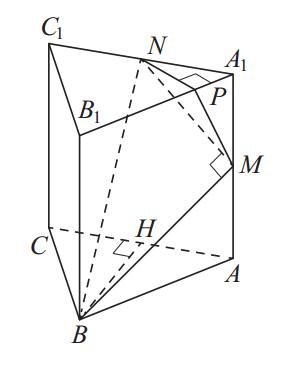
Тогда 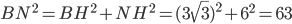 . Вместе с тем,
. Вместе с тем, 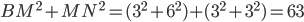 , а тогда по теореме, обратной теореме Пифагора, треугольник BMN - прямоугольный с прямым углом BMN.
, а тогда по теореме, обратной теореме Пифагора, треугольник BMN - прямоугольный с прямым углом BMN.
б) Проведем перпендикуляр NP к прямой 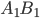 . Так как NP перпендикулярно
. Так как NP перпендикулярно 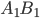 и
и 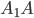 , то NP перпендикулярно
, то NP перпендикулярно 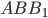 . Поэтому MP - проекция MN на плоскость
. Поэтому MP - проекция MN на плоскость 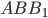 . Прямая BM перпендикулярна MN, тогда по теореме о трех перпендикулярах BM перпендикулярно MP. Значит, угол NMP - линейный угол искомого угла.
. Прямая BM перпендикулярна MN, тогда по теореме о трех перпендикулярах BM перпендикулярно MP. Значит, угол NMP - линейный угол искомого угла.
Длина NP равна половине высоты треугольника 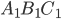 , то есть
, то есть 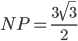 . Поэтому
. Поэтому 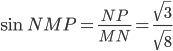 . Следовательно, угол NMP равен arcsin
. Следовательно, угол NMP равен arcsin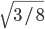 .
.
15. Пусть 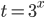 . Тогда
. Тогда 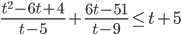

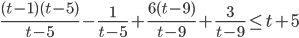 , откуда
, откуда 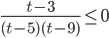

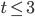 или
или 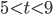 .
.
При 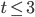 :
: 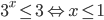 .
.
При 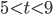 :
: 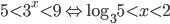 .
.
16. а) Обозначим центры окружностей 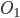 и
и 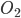 соответственно. Пусть общая касательная, проведенная к окружности в точке K, пересекает AB в точке M. По свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
соответственно. Пусть общая касательная, проведенная к окружности в точке K, пересекает AB в точке M. По свойству касательных, проведенных из одной точки, AM = KM и KM = BM.  Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный. Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD перпендикулярно AB. Аналогично получаем, что BC перпендикулярно AB. Следовательно, прямые AD и BC параллельны.
Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный. Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD перпендикулярно AB. Аналогично получаем, что BC перпендикулярно AB. Следовательно, прямые AD и BC параллельны.
б) Пусть для определенности первая окружность имеет радиус 4, вторая - радиус 1. Треугольники BKC и AKD подобны, AD:BC = 4:1. Пусть 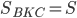 , тогда
, тогда 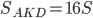 .
.
У треугольников AKD и AKB общая высота, следовательно, 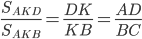 , то есть
, то есть 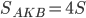 . Аналогично,
. Аналогично, 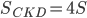 .
.
Площадь трапеции ABCD равна 25S. Проведем к AD перпендикуляр 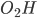 , равный высоте трапеции, и найдем его длину из прямоугольного треугольника
, равный высоте трапеции, и найдем его длину из прямоугольного треугольника 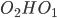 по теореме Пифагора
по теореме Пифагора 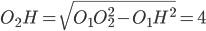 . Тогда
. Тогда 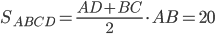 . Значит,
. Значит, 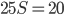 и
и 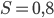 ,
, 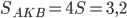 .
.
17. По условию, долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
1; 0,6; 0,4; 0,3; 0,2; 0,1; 0.
Пусть 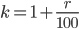 , тогда долг на 1-е число каждого месяца равен:
, тогда долг на 1-е число каждого месяца равен:
k ; 0,6k ; 0,4k ; 0,3k ; 0,2k ; 0,1k .
Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:
k − 0,6; 0,6k − 0,4 ; 0,4k − 0,3 ; 0,3k − 0,2 ; 0,2k − 0,1; 0,1k .
Общая сумма выплат составляет:
k(1+0,6+0,4+0,3+0,2+0,1)-(0,6+0,4+0,3+0,2+0,1)=2,6(k-1)+1.
По условию, общая сумма выплат будет меньше 1,2 млн рублей, значит,
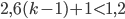 ;
; 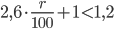 ;
; 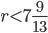 .
.
Наибольшее целое решение этого неравенства — число 7. Значит, искомое число процентов равно 7.
18. www.itmathrepetitor.ru Если 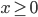 , то уравнение
, то уравнение 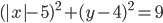 задает окружность
задает окружность 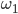 с центром в точке
с центром в точке 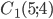 радиусом 3, а если
радиусом 3, а если 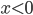 , то оно задает окружность
, то оно задает окружность 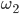 с центром в точке
с центром в точке 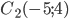 с таким же радиусом.
с таким же радиусом.  При положительных значениях
При положительных значениях  уравнение
уравнение 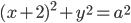 задает окружность
задает окружность 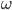 с центром в точке
с центром в точке 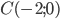 радиусом
радиусом  . Поэтому задача состоит в том, чтобы найти все значения
. Поэтому задача состоит в том, чтобы найти все значения  , при каждом из которых окружность
, при каждом из которых окружность 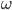 имеет единственную общую точку с объединением окружностей
имеет единственную общую точку с объединением окружностей 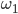 и
и 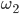 .
.
Из точки 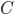 проведем луч
проведем луч 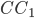 и обозначим через
и обозначим через 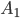 и
и 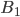 точки его пересечения с окружностью
точки его пересечения с окружностью 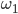 , где
, где 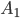 лежит между
лежит между 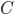 и
и 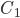 . Так как
. Так как 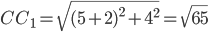 , то
, то 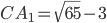 ,
, 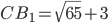 .
.
При 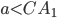 или
или 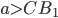 окружности
окружности 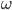 и
и 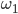 не пересекаются.
не пересекаются.
При 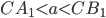 окружности
окружности 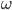 и
и 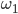 имеют две общие точки.
имеют две общие точки.
При 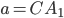 или
или 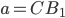 окружности
окружности 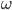 и
и 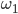 касаются.
касаются.
Из точки 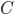 проведем луч
проведем луч 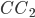 и обозначим через
и обозначим через 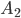 и
и 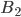 точки его пересечения с окружностью
точки его пересечения с окружностью 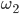 , где
, где 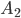 лежит между
лежит между 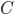 и
и 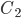 . Так как
. Так как 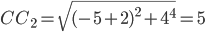 , то
, то 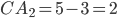 ,
, 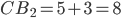 .
.
www.itmathrepetitor.ru При 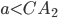 или
или 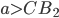 окружности
окружности 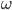 и
и 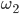 не пересекаются.
не пересекаются.
При 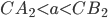 окружности
окружности 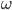 и
и 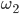 имеют две общие точки.
имеют две общие точки.
При 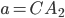 или
или 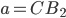 окружности
окружности 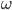 и
и 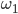 касаются.
касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность 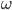 касается ровно одной из двух окружностей
касается ровно одной из двух окружностей 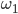 и
и 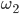 и не пересекается с другой. Так как
и не пересекается с другой. Так как 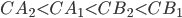 , то условию задачи удовлетворяют только числа
, то условию задачи удовлетворяют только числа 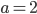 и
и 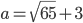 .
.
смотрите также Демо ЕГЭ 2017 Базовый уровень