Решение демонстрационного варианта
контрольных измерительных материалов
для проведения в 2018 году основного государственного экзамена
по МАТЕМАТИКЕ

Условия задач и ответы здесь
21. Уравнение приводится к виду 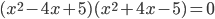 . Откуда
. Откуда 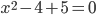 или
или 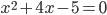 . Первое уравнение корней не имеет, второе уравнение имеет корни
. Первое уравнение корней не имеет, второе уравнение имеет корни 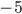 и
и  . Как решать квадратные уравнения
. Как решать квадратные уравнения
22. www.itmathrepetitor.ru Пусть искомое расстояние равно  км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно 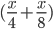 часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение: 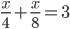 . Решив уравнение, получим
. Решив уравнение, получим 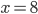 .
.
23. Разложим числитель дроби на множители: 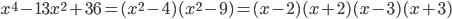 . При
. При 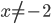 и
и 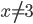 функция принимает вид
функция принимает вид 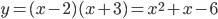 . Ее график - парабола, из которой выколоты точки
. Ее график - парабола, из которой выколоты точки 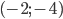 и
и 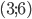 . Прямая
. Прямая 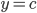 имеет с графиком ровно одну общую точку либо когда проходит через вершину параболы, либо когда пересекает параболу в двух точках, одна из которых выколота.
имеет с графиком ровно одну общую точку либо когда проходит через вершину параболы, либо когда пересекает параболу в двух точках, одна из которых выколота.  Вершина параболы имеет координаты
Вершина параболы имеет координаты 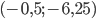 . Поэтому
. Поэтому 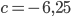 ,
, 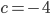 или
или 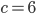 .
.
24. 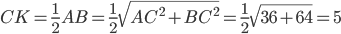

25. Треугольники BEC и AED равны по трем сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180o, то углы равны 90o. Такой параллелограмм является прямоугольником. 
26. Пусть 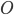 -центр данной окружности, а
-центр данной окружности, а 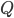 - центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. Лучи AQ и AO - биссектрисы смежных углов, значит, угол OAQ прямой.
- центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. Лучи AQ и AO - биссектрисы смежных углов, значит, угол OAQ прямой.  Из прямоугольного треугольника OAQ получаем:
Из прямоугольного треугольника OAQ получаем: 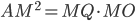 . Значит,
. Значит, 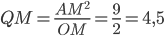
смотрите также Пробный вариант ОГЭ (ГИА) 2016 Санкт-Петербург и ОГЭ Демо 2017