Сканави М.И.
Задачи по планиметрии с ответами и решениями

Группа А. Задачи 1 - 50 (с ответами и решениями)
-
Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найти катеты треугольника. Ответ: 42 см, 56 см Решение
-
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна m и делит прямой угол в отношении 1:2. Найти стороны треугольника. Ответ:
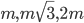 Решение
Решение -
Длины сторон прямоугольного треугольника образуют арифметическую прогрессию с разностью 1 см. Найти длину гипотенузы. Ответ: 5 см Решение
-
Определить острые углы прямоугольного треугольника, если медиана, проведенная к его гипотенузе, делит прямой угол в отношении 1:2. Ответ: 60о и 30о Решение
-
Катеты прямоугольного треугольника равны 9 и 12 см. Найти расстояние между точкой пересечения его биссектрис и точкой пересечения медиан. Ответ: 1 см Решение
-
Найти биссектрисы острых углов прямоугольного треугольника с катетами 24 и 18 см. Ответ:
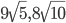 Решение
Решение -
В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника. Ответ: 54 Решение
-
Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 м проведен перпендикуляр к гипотенузе. Вычислить площади образовавшихся треугольников. Ответ: 8,64 и 15,36 Решение
-
Площадь прямоугольного треугольника равна
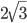 см2. Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1:2. Ответ:
см2. Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1:2. Ответ: 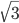 Решение
Решение -
В равнобедренном треугольнике с боковой стороной, равной 4 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3 см. Ответ:
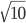 Решение
Решение -
Основание равнобедренного треугольника равно
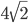 см, а медиана боковой стороны 5 см. Найти длины боковых сторон. Ответ: 6 Решение
см, а медиана боковой стороны 5 см. Найти длины боковых сторон. Ответ: 6 Решение - Найти длины сторон равнобедренного треугольника ABC с основанием АС, если известно, что длины его высот AN и ВМ равны соответственно n и m. Ответ:
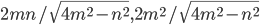 Решение
Решение -
В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20 см. Найти биссектрису угла при основании треугольника. Ответ: 6 Решение
-
Вычислить площадь равнобедренного треугольника, если длина высоты, проведенной к боковой стороне, равна 12 см, а длина основания равна 15 см. Ответ: 75 Решение
-
Найти площадь равнобедренного треугольника, если основание его равно а, а длина высоты, проведенной к основанию, равна длине отрезка, соединяющего середины основания и боковой стороны. Ответ:
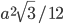 Решение
Решение -
Высота, проведенная к основанию равнобедренного треугольника, равна Н и вдвое больше своей проекции на боковую сторону. Найти площадь треугольника. Ответ:
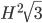 Решение
Решение -
Найти длины сторон АВ и АС треугольника ABC, если ВС = 8 см, а длины высот, проведенных к АС и ВС, равны соответственно 6,4 и 4 см. Ответ:
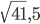 Решение
Решение -
В треугольнике длины двух сторон составляют 6 и 3 см. Найти длину третьей стороны, если полусумма высот, проведенных к данным сторонам, равна третьей высоте. Ответ: 4 Решение
-
Длина основания треугольника равна 36 см. Прямая, параллельная основанию, делит площадь треугольника пополам. Найти длину отрезка этой прямой, заключенного между сторонами треугольника. Ответ:
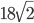 Решение
Решение -
На каждой медиане треугольника взята точка, делящая медиану в отношении 3:1, считая от вершины. Во сколько раз площадь треугольника с вершинами в этих трех точках меньше площади исходного треугольника? Ответ: 64 Решение
-
Прямая, параллельная основанию треугольника, делит его на части, площади которых относятся как 2:1. В каком отношении, считая от вершины, она делит боковые стороны? Ответ:
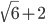 или
или 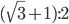 Решение
Решение -
Основание треугольника равно 30 см, а боковые стороны 26 и 28 см. Высота разделена в отношении 2:3 (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Определить площадь полученной при этом трапеции. Ответ: 282,24 Решение
-
Из точки А, не лежащей на окружности, проведены к ней касательная и секущая. Расстояние от точки А до точки касания равно 16 см, а до одной из точек пересечения секущей с окружностью равно 32 см. Найти радиус окружности, если секущая удалена от ее центра на 5 см. Ответ: 13 Решение
-
Из внешней точки проведены к окружности секущая длиной 12 см и касательная, длина которой составляет 2/3 внутреннего отрезка секущей. Определить длину касательной. Ответ: 6 Решение
-
Хорда окружности равна 10 см. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Определить радиус окружности, если внутренний отрезок секущей равен 12 см. Ответ: 6,25 Решение
- Две окружности радиусов R = 3 см и r = 1 см касаются внешним образом. Найти расстояния от точки касания окружностей до их общих касательных. Ответ: 0; 1,5 Решение
- Из одной точки проведены к окружности две касательные. Длина каждой касательной 12 см, а расстояние между точками касания 14,4 см. Определить радиус окружности. Ответ: 9 Решение
- В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен r. Найти радиус большей окружности. Ответ: 3r Решение
- Через концы дуги окружности, содержащей 120°, проведены касательные, и в фигуру, ограниченную этими касательными и данной дугой, вписана окружность. Доказать, что ее длина равна длине исходной дуги. Решение
- В окружности проведены две хорды АВ=а и АС=b. Длина дуги АС вдвое больше длины дуги АВ. Найти радиус окружности. Ответ:
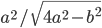 Решение
Решение - Общая хорда двух пересекающихся окружностей видна из их центров под углами 90o и 60o. Найти радиусы окружностей, если расстояние между их центрами равно
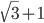 . Ответ: 2;
. Ответ: 2; 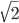 Решение
Решение - В сектор АОВ с радиусом R и углом 90° вписана окружность, касающаяся отрезков ОА, ОB и дуги АВ. Найти радиус окружности. Ответ:
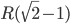 Решение
Решение - Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. Каковы длины отрезков, на которые делится хорда точкой Р? Ответ: 12; 6 Решение
- В окружности радиуса г проведена хорда, равная r/2. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Найти расстояние между касательной и секущей. Ответ: r/8 Решение
- В большем из двух концентрических кругов проведена хорда, равная 32 см и касающаяся меньшего круга. Определить длину радиуса каждого из кругов, если ширина образовавшегося кольца равна 8 см. Ответ: 12; 20 Решение
- Круг радиуса R разделен двумя концентрическими с ним окружностями на три равновеликие фигуры. Найти радиусы этих окружностей. Ответ:
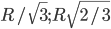 Решение
Решение - Площадь кругового кольца равна S. Радиус большей окружности равен длине меньшей окружности. Определить радиус последней. Ответ:
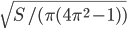 Решение
Решение - Определить площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны С1 и С2 (С1>С2). Ответ:
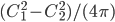 Решение
Решение - Хорда АВ постоянной длины скользит своими концами по окружности радиуса R. Точка О этой хорды, находящаяся на расстояниях а и b от концов А и В хорды, описывает при полном обороте окружность. Вычислить площадь кольца, заключенного между данной окружностью и окружностью, описанной точкой С. Ответ:
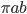 Решение
Решение - Внутри круга радиуса 15 см взята точка М на расстоянии 13 см от центра. Через точку М проведена хорда длиной 18 см. Найти длины отрезков, на которые точка М делит хорду. Ответ: 4 Решение
- В круговой сектор с центральным углом в 120° вписан круг. Найти радиус описанного круга, если радиус данного круга равен R. Ответ:
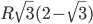 Решение
Решение - В круговой сектор, дуга которого содержит 60°, вписан круг. Найти отношение площади этого круга к площади сектора. Ответ: 2:3 Решение
- Круг радиуса R обложен четырьмя равными кругами, касающимися данного так, что каждые два соседних из этих четырех кругов касаются друг друга. Вычислить площадь одного из этих кругов. Ответ:
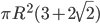 Решение
Решение - Три окружности разных радиусов попарно касаются друг друга. Прямые, соединяющие их центры, образуют прямоугольный треугольник. Найти радиус меньшей окружности, если радиусы большей и средней окружностей равны 6 и 4 см. Ответ: 2 Решение
- Три равные окружности радиуса r попарно касаются одна другой. Вычислить площадь фигуры, расположенной вне окружностей и ограниченной их дугами, заключенными между точками касания. Ответ:
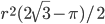 Решение
Решение - Общей хордой двух кругов стягиваются дуги в 60 и 120°. Найти отношение площадей этих кругов. Ответ: 3:1 Решение
- Доказать, что если диаметр полукруга разделить на две произвольные части и на каждой из них построить как на диаметре полуокружность (внутри данного полукруга), то площадь, заключенная между тремя полуокружностями, равна площади круга, диаметр которого равен длине перпендикуляра к диаметру полукруга, проведенного в точке деления до пересечения с окружностью. Решение
- Определить площадь круга, вписанного в сектор круга радиуса R с хордой a. Ответ:
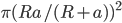 Решение
Решение - Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислить площадь отсекаемого ею сегмента. Ответ:
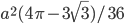 Решение
Решение - Сторона квадрата, вписанного в окружность, равна а. Вычислить площадь отсекаемого ею сегмента. Ответ:
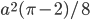 Решение
Решение