Сканави М.И.
Задачи по планиметрии с ответами и решениями

Группа А. Задачи 151 - 190 (с ответами и решениями)
-
Вычислить площадь трапеции по разности оснований, равной 14 см, и двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность. Ответ:
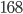 Решение
Решение -
В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон. Ответ:
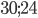 Решение
Решение - Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
- Трапеция разбита диагоналями на четыре треугольника. Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ:
 Решение
Решение - Диагональ прямоугольной трапеции и ее боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см. Ответ:
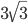 Решение
Решение - Вычислить площадь прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно
 , а большая боковая сторона равна
, а большая боковая сторона равна  . Ответ:
. Ответ: 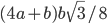 Решение
Решение - Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12 см2, а длина высоты равна 2 см. Ответ:
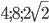 Решение
Решение - Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны соответственно 8 см, 14 см и 44 см2. Ответ:
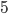 Решение
Решение - Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции. Ответ:
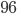 Решение
Решение - В равнобедренной трапеции одно основание равно 40 см, а другое 24 см. Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ:
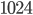 Решение
Решение - В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции. Ответ:
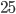 Решение
Решение - Большее основание'трапеции в 2 раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношение высоты каждой из двух полученных трапеций к высоте трапеции. Ответ:
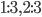 Решение
Решение - Основания равнобедренной трапеции
 и
и  , боковая сторона ее равна
, боковая сторона ее равна  , а диагональ равна
, а диагональ равна 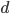 . Доказать, что
. Доказать, что 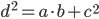 .
. - Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ:
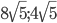 Решение
Решение - В равнобедренной трапеции даны основания
 =21 см,
=21 см,  = 9 см и высота
= 9 см и высота 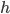 = 9 см. Найти радиус описанного круга. Ответ:
= 9 см. Найти радиус описанного круга. Ответ: 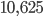 Решение
Решение - В окружность радиуса
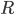 вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции. Ответ:
вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции. Ответ: 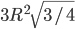 Решение
Решение - Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности, описанной около трапеции, если известно, что ее средняя линия равна высоте. Ответ:
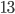 Решение
Решение - Найти площадь равнобедренной трапеции, если ее высота равна
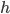 , а боковая сторона видна из центра описанной окружности под углом 60°. Ответ:
, а боковая сторона видна из центра описанной окружности под углом 60°. Ответ: 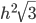 Решение
Решение - Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найти основания трапеции. Ответ:
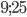 Решение
Решение - Площадь равнобедренной трапеции, описанной около круга, равна
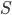 , а высота трапеции в 2 раза меньше ее боковой стороны. Определить радиус вписанного круга. Ответ:
, а высота трапеции в 2 раза меньше ее боковой стороны. Определить радиус вписанного круга. Ответ: 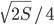 Решение
Решение - Площадь равнобедренной трапеции, описанной около круга, равна
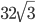 см2. Определить боковую сторону трапеции, если известно, что острый угол при основании равен
см2. Определить боковую сторону трапеции, если известно, что острый угол при основании равен 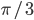 . Ответ:
. Ответ: 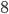 Решение
Решение - Площадь равнобедренной трапеции, описанной около круга, равна 8 см2. Определить стороны трапеции, если угол при основании содержит 30°. Ответ:
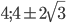 Решение
Решение - Площадь равнобедренной трапеции, описанной около круга, равна
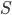 . Определить боковую сторону трапеции, если известно, что острый угол при основании равен
. Определить боковую сторону трапеции, если известно, что острый угол при основании равен 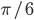 . Ответ:
. Ответ: 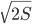 Решение
Решение - Площадь равнобедренной трапеции, описанной около круга, равна
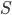 . Определить радиус круга, если угол при основании трапеции равен 30°. Ответ:
. Определить радиус круга, если угол при основании трапеции равен 30°. Ответ: 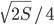 Решение
Решение - В равнобедренную трапецию вписана окружность радиуса
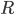 . Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь трапеции. Ответ:
. Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь трапеции. Ответ: 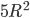 Решение
Решение - Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно
 , а угол при меньшем основании равен 120°. Ответ:
, а угол при меньшем основании равен 120°. Ответ: 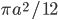 Решение
Решение - В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной n и m. Определить площадь трапеции. Ответ:
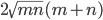 Решение
Решение - В равнобедренную трапецию вписан круг. Доказать, что отношение площади круга к площади трапеции равно отношению длины окружности к периметру трапеции.
- Равносторонний шестиугольник ABCDEF состоит из двух трапеций, имеющих общее основание CF. Известно, что АС = 13 см, АЕ = 10 см. Найти площадь шестиугольника. Ответ:
 Решение
Решение - Найти сторону правильного шестиугольника, равновеликого равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ:
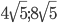 Решение
Решение - Вычислить отношение площадей квадрата, правильного треугольника и правильного шестиугольника, вписанных в одну и ту же окружность. Ответ:
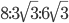 Решение
Решение - Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, длины сторон которых равны. Ответ:
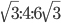 Решение
Решение - В правильный треугольник со стороной, равной
 , вписана окружность, в которую вписан правильный шестиугольник. Найти площадь шестиугольника. Ответ:
, вписана окружность, в которую вписан правильный шестиугольник. Найти площадь шестиугольника. Ответ: 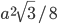 Решение
Решение - Около квадрата, сторона которого равна
 , описана окружность, а около окружности — правильный шестиугольник. Определить площадь шестиугольника. Ответ:
, описана окружность, а около окружности — правильный шестиугольник. Определить площадь шестиугольника. Ответ: 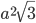 Решение
Решение - Из точки М, находящейся на расстоянии
 от окружности, приведена к этой окружности касательная длиной
от окружности, приведена к этой окружности касательная длиной 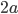 . Найти площадь правильного шестиугольника, вписанного в окружность. Ответ:
. Найти площадь правильного шестиугольника, вписанного в окружность. Ответ: 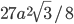 Решение
Решение - В правильный треугольник вписана окружность, а в нее — правильный шестиугольник. Найти отношение площадей треугольника и шестиугольника. Ответ:
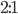 Решение
Решение - На сторонах равностороннего треугольника вне его построены квадраты. Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если сторона данного треугольника равна
 . Ответ:
. Ответ: 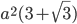 Решение
Решение - В правильный шестиугольник, сторона которого равна
 , вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями. Ответ:
, вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями. Ответ: 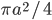 Решение
Решение - Данный квадрат со стороной
 срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника. Ответ:
срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника. Ответ: 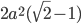 Решение
Решение - Доказать, что сумма расстояний от любой точки, взятой внутри правильного шестиугольника, до всех прямых, содержащих его стороны, есть величина постоянная.