Производная функции

перейти к содержанию справочника

Правила дифференцирования

$(C\cdot f(x))'=C\cdot f'(x)$

$(f(x)\pm g(x))'=f'(x)\pm g'(x)$

$(f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x)$

$\left(\displaystyle\frac{f(x)}{g(x)}\right)'=\displaystyle\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g^2(x)}$

$(g(f(x)))'=g'(f(x))\cdot f'(x)$

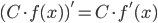
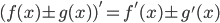
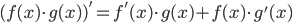
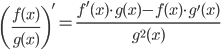
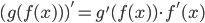
Производные элементарных функций

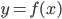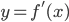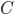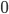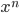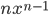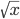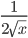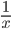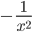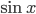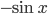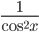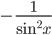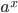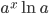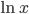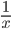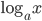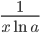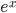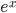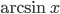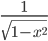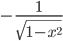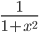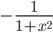Если функция 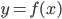$y=f(x)$ имеет производную в точке 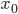$x_0$, то уравнение касательной в точке 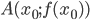$A(x_0; f(x_0))$ имеет вид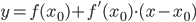 $y=f(x_0)+f'(x_0)\cdot (x-x_0)$

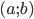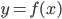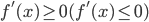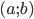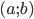Для того чтобы дифференцируемая на $(a;b)$ функция $y=f(x)$ не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы $f'(x)\geq 0 (f'(x)\leq 0)$ для всех $x$ из интервала $(a;b)$. Если же для любого $x$ из $(a;b)$ известно, что 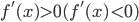$f'(x)>0 (f'(x)<0)$, то функция 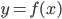$y=f(x)$ возрастает (убывает) на этом интервале.