Решение текстовых задач на числовые зависимости

Задачи 5 - 7
Весь список текстовых задач на числовые зависимости здесь.
- Условие задачи: При каких натуральных
 число
число 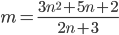 также будет натуральным?
также будет натуральным?
Решение: Выделим целую часть рациональной дроби. Проще всего это сделать, если разделить числитель дроби на знаменатель "уголком". Получаем: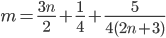 . Для того чтобы избавиться от дробей в целой части, умножим обе части равенства на 4:
. Для того чтобы избавиться от дробей в целой части, умножим обе части равенства на 4: 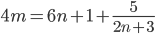 .
.
Число 5 имеет делители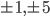 . Проверим случаи: а)
. Проверим случаи: а) 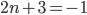 , тогда
, тогда 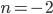 - не является натуральным числом. б)
- не является натуральным числом. б) 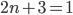 , тогда
, тогда 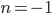 - не натуральное. в)
- не натуральное. в) 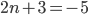 , тогда
, тогда 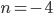 - не натуральное. г)
- не натуральное. г) 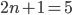 , тогда
, тогда 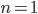 - натуральное,
- натуральное, 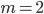 - натуральное.
- натуральное.
Ответ: 1 - Условие задачи: При каких натуральных
 дробь
дробь 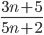 сократима?
сократима?
Решение: Условие сократимости дает систему из уравнений: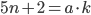 и
и 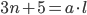 , где
, где 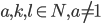 .
.
Из первого уравнения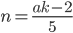 . Подставим
. Подставим  во второе уравнение и получим, что
во второе уравнение и получим, что 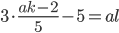 .
.
Приведем подобные слагаемые. Тогда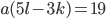 . Так как справа стоит простое число 19, а слева произведение двух целых чисел, то или
. Так как справа стоит простое число 19, а слева произведение двух целых чисел, то или 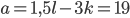 , или
, или 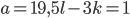 . Первый случай невозможен, так как это означает, что исходная дробь несократима. Значит, дробь сокращается на 19. Осталось выяснить, при каких
. Первый случай невозможен, так как это означает, что исходная дробь несократима. Значит, дробь сокращается на 19. Осталось выяснить, при каких  это выполняется.
это выполняется.
Из второго уравнения следует, что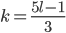 . Далее выделим целую часть дроби:
. Далее выделим целую часть дроби: 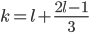 . Так как
. Так как 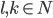 , то
, то 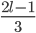 должно быть целым, то есть
должно быть целым, то есть 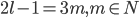 . Следовательно,
. Следовательно, 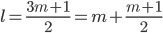 . Рассуждая аналогично, имеем, что
. Рассуждая аналогично, имеем, что 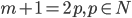 , значит,
, значит, 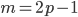 . Итак, при
. Итак, при 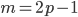 ,
,  , дробь
, дробь 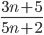 сократима. Однако в ответе нужно указать вид числа
сократима. Однако в ответе нужно указать вид числа  . Так как
. Так как 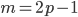 , то
, то 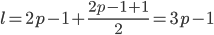 . Значит,
. Значит, 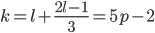 и
и 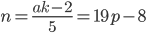
Ответ: при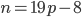 ,
, 
- Условие задачи: Сумма квадратов крайних чисел четырехзначного числа M равна 58. Сумма квадратов средних цифр этого числа равна 68. Сумма числа M и числа 4536 равна числу, записанному теми же цифрами числа М, но в обратном порядке. Найдите число M.
Решение: Пусть число имеет вид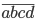 . Тогда
. Тогда 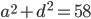 ,
, 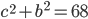 . И
. И 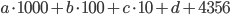
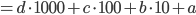 . Складывая числа в разряде единиц, слева получим два возможных варианта:
. Складывая числа в разряде единиц, слева получим два возможных варианта: 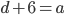 (если
(если 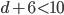 ) или
) или 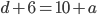 (если
(если 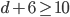 ). В первом случае получаем, что
). В первом случае получаем, что 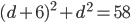 и
и 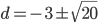 - не целое. Во втором случае:
- не целое. Во втором случае: 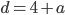 и
и 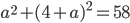 , откуда
, откуда 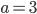 . Тогда
. Тогда 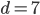 .
.
Аналогично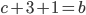 или
или 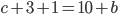 . В первом случае получаем, что
. В первом случае получаем, что 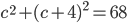 и
и 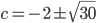 - не подходит. Во втором случае
- не подходит. Во втором случае 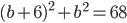 и
и 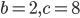 .
.
Ответ: 3287