Олимпиадные текстовые задачи

перейти к содержанию курса текстовых задач

1. В конференции участвовали 100 человек – химиков и алхимиков. Каждому был задан вопрос: «Если не считать Вас, то кого больше среди остальных участников – химиков или алхимиков?». Когда опросили 51 участника, и все ответили, что алхимиков больше, опрос прервался. Алхимики всегда лгут, а химики всегда говорят правду. Сколько химиков среди участников? Решение

2. На собрании лжецов и рыцарей путешественник пытается определить самого старшего. Ему известно, что среди присутствующих лжецов и рыцарей поровну, а также, что возрасты всех различны. Ему разрешается выбрать любую группу людей (содержащую не менее двух человек) и спросить любого из присутствующих, кто в этой группе самый старший. Покажите, что путешественник не сможет гарантированно определить самого старшего, сколько бы вопросов он ни задавал. (Рыцари всегда говорят правду, лжецы всегда лгут). Решение
3. Можно ли соединить пять городов дорогами так, чтобы каждый город был соединен с тремя другими? Решение
4. Три спортсмена – А, В, С участвовали в забеге. Известно, что С задержался на старте и выбежал последним, а В – вторым. Во время бега С 6 раз менялся местами с другими участниками, а А – 5 раз. Еще известно, что В финишировал раньше А. В каком порядке финишировали спортсмены? Решение
5. Типографии поручили набрать и напечатать 3 книги: А, В  и С. В ее распоряжении имеются две машины: одна для набора, другая для печатания. На набор текста каждой книги уходит 3 ч. На печатание книги А надо 2 ч, книги В – 4 ч и книги С – 1 ч. Как следует организовать работу, чтобы закончить изготовление книг как можно скорее? Решение
6. В некотором государстве каждые двое – либо друзья, либо враги. Каждый человек может в некоторый момент поссориться со всеми друзьями и помириться со всеми врагами. Оказалось, что каждые три человека могут таким образом стать друзьями. Докажите, что тогда и все люди в государстве могут стать друзьями. Решение
7. В клетки таблицы размером 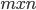$m x n$ вписаны некоторые числа. Разрешается одновременно менять знак у всех чисел одного столбца или одной строки. Докажите, что после нескольких таких операций над любой таблицей можно добиться того, что суммы чисел, стоящих в любой строке и в любом столбце, будут неотрицательными. Решение
8. В некоторой стране из каждого города выходит нечетное число дорог, соединяющих его с другими городами этой страны. На центральной площади каждого города поднят чёрный или белый флаг. Каждое утро в одном из городов, у которого число соседей с флагами другого цвета больше половины, меняют цвет флага. Может ли этот процесс продолжаться бесконечно? Решение
9. В стране, где 25 городов, три авиакомпании хотят, чтобы для любой пары городов все беспосадочные авиарейсы между этими городами осуществлялись только одной из авиакомпаний, однако любая авиакомпания могла доставлять пассажиров из любого города в любой другой с посадкой не более чем в одном промежуточном городе. Возможно ли это? Решение
10. Перед детьми две кучки орехов. Девочка и мальчик придумали такую игру: каждый из них по очереди одну кучку орехов перекладывает на тарелку, а другую делит на две меньшие кучки. Проигрывает тот, кто при своем очередном ходе не сможет разделить кучку, так как в ней остался только один орех. Девочка начинает первой. Как она должна играть, чтобы выиграть, если в начале игры в одной из кучек было 24 ореха, а в другой 19?  Решение
11. Играют двое. Начинающий называет одно из чисел: 1, 2, 3, 4. Второй игрок прибавляет к этому числу одно из этих же чисел: 1, 2, 3, 4 и называет вслух получившуюся сумму. То же самое делает затем первый игрок и т. д. Победителем считается тот, кто первым назовет число 40. Как надо играть, чтобы выиграть? Решение
12. В ящике лежат 35 шариков. Двое играющих по очереди вынимают их из ящика, причем по условию игры каждый обязан вынуть в свой ход не менее одного шарика и не более пяти. Проигравшим считается тот, кто вынужден будет своим ходом вынуть из ящика последний шар. Может ли игрок, делающий ход первым, обеспечить себе выигрыш? Каким образом? Решение

Задачи для самостоятельного решения

1. В парламенте у каждого депутата не более трех врагов. Докажите, что парламент можно разделить на две палаты так, что у каждого депутата в своей палате будет не более одного врага.
2. Житель страны N. считается богатым, если его месячный доход выше зарплаты министра финансов, в противном случае — небогатым. Известно, что богатые мужчины предпочитают небогатых женщин. Докажите, что если доходы у всех разные, то можно установить министру финансов такую зарплату, чтобы в стране стало поровну богатых мужчин и небогатых женщин.
3. На столе стоят три пустых банки из-под меда. Винни-Пух, Кролик и Пятачок по очереди кладут по одному ореху в одну из банок. Их порядковые номера до начала игры определяются жребием. При этом Винни может добавлять орех только в первую или вторую банку, Кролик – только во вторую или в третью, а Пятачок – в первую или третью. Тот, после чьего хода в какой-нибудь банке оказалось ровно 1999 орехов, проигрывает. Докажите, что Винни-Пух и Пятачок могут, договорившись, играть так, чтобы Кролик проиграл.
4. 100 карточек в стопке пронумерованы (от 1 до 100) сверху вниз. Двое играющих по очереди снимают сверху по одной или несколько карточек и отдают противнику. Выигрывает тот, у кого первого произведение номеров  всех карточек станет кратно 1000000. Кто из игроков может гарантировать себе выигрыш? Ответ: первый игрок
5. Таня задумала целое число от 1 до 100, которое Саша пытается угадать. В случае его удачи Таня говорит: «Угадал!». В случае неудачи Таня число меняет: делит на Сашино, если делится нацело, а если не делится, то умножает на Сашино число и прибавляет единицу (не сообщая ему ничего). Докажите, что Саша сможет угадать Танино число.
6. В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя – либо два, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре? Ответ: Петя
7. Среди 101 монеты – 50 фальшивых. Каждая фальшивая монета тяжелее настоящей на 1 г. Имеются также двухчашечные весы со стрелкой, показывающей разность масс на чашках. Петя взял одну монету и за одно взвешивание хотел бы определить, фальшивая она или нет. Сможет ли он это сделать? Ответ: да