Текстовые задачи. Задачи с целочисленными неизвестными

перейти к содержанию курса текстовых задач
-
Школьник переклеивает свои марки в новый альбом. Если он будет наклеивать на каждый лист по 20 марок, то ему не хватит этого альбома, а если по 23 марки на лист, то по крайней мере один лист останется пустым. Если же в дополнение к старому альбому он возьмет новый, на каждом листе которого наклеено по 21 марке, то всего станет 500 марок. Сколько листов в новом альбоме? Решение
-
Возле дома запланировано посадить более 15 лип и берез. Если число лип увеличить вдвое, а число берез увеличить на 18, то берез станет больше. Если же число берез увеличить вдвое, не меняя число лип, то лип все равно будет больше. Сколько лип и сколько берез планируется посадить возле дома? Решение
-
В автогонках принимают участие команды, имеющие одинаковое число автомобилей марки «Волга» и марки «Москвич», причем в каждой команде число всех автомобилей меньше
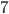 . Если в каждой команде число автомобилей марки «Волга» оставить без изменения, а число автомобилей марки «Москвич» увеличить в
. Если в каждой команде число автомобилей марки «Волга» оставить без изменения, а число автомобилей марки «Москвич» увеличить в 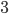 раза, то общее число «Москвичей», участвующих в гонках, будет на
раза, то общее число «Москвичей», участвующих в гонках, будет на 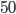 больше общего числа «Волг», а число автомобилей в каждой команде превысит 12. Определить число команд, участвующих в гонках, и число «Волг» и «Москвичей» в каждой команде. Решение
больше общего числа «Волг», а число автомобилей в каждой команде превысит 12. Определить число команд, участвующих в гонках, и число «Волг» и «Москвичей» в каждой команде. Решение -
Группа студентов, состоящая из 30 человек, получила на экзамене оценки «2», «3», «4», «5». Сумма полученных оценок равна
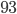 , причем троек было больше, чем пятерок, и меньше, чем четверок. Кроме того, число четверок делилось на 10, а число пятерок было четным. Сколько каких оценок получили студенты группы? Решение
, причем троек было больше, чем пятерок, и меньше, чем четверок. Кроме того, число четверок делилось на 10, а число пятерок было четным. Сколько каких оценок получили студенты группы? Решение -
Из города A в город B отправился путешественник, который в первый день преодолел
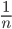 часть всего пути. На следующий день он прошел
часть всего пути. На следующий день он прошел 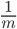 оставшегося пути. В последующие дни он проходил попеременно то
оставшегося пути. В последующие дни он проходил попеременно то 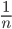 часть, то
часть, то 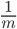 часть пути, оставшегося к концу предыдущего дня. Через 10 дней такого путешествия выяснилось, что он прошел
часть пути, оставшегося к концу предыдущего дня. Через 10 дней такого путешествия выяснилось, что он прошел 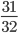 всего расстояния между городами. Найти числа
всего расстояния между городами. Найти числа  и
и  , если известно, что они целые, причем
, если известно, что они целые, причем 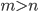 . Решение
. Решение -
Встречаются две команды шахматистов A и B. По условиям соревнований каждый участник одной команды играет по одной партии с каждым участником другой команды. Общее число предстоящих партий в
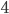 раза больше числа всех игроков в обеих командах.Однако из-за болезни два игрока не смогли явиться на матч, в связи с чем число всех сыгранных в матче партий оказалось на 17 меньше предполагавшегося. Сколько игроков выступило в матче за команду A, если известно, что в ней было меньше игроков, чем в команде B? Решение
раза больше числа всех игроков в обеих командах.Однако из-за болезни два игрока не смогли явиться на матч, в связи с чем число всех сыгранных в матче партий оказалось на 17 меньше предполагавшегося. Сколько игроков выступило в матче за команду A, если известно, что в ней было меньше игроков, чем в команде B? Решение
Задачи для самостоятельного решения
- Рабочий изготовил некоторое количество деталей видов A и B, причем деталей A он изготовил больше, чем деталей B. Если он изготовит деталей A в
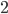 раза больше, то общее число деталей станет меньше
раза больше, то общее число деталей станет меньше 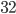 , а если деталей B в
, а если деталей B в 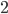 раза больше, то общее число деталей станет больше
раза больше, то общее число деталей станет больше 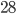 . Сколько деталей A и сколько деталей B изготовил рабочий? Ответ: 11 А; 9 В
. Сколько деталей A и сколько деталей B изготовил рабочий? Ответ: 11 А; 9 В - Принятых в институт первокурсников первоначально распределили поровну по учебным группам. В связи с сокращением числа специальностей количество групп уменьшилось на
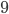 . Тогда всех первокурсников перераспределили по новым группам, причем так, что группы снова получились равные по численности. Известно, что всего есть 1512 первокурсников и число студентов в группе оказалось меньше
. Тогда всех первокурсников перераспределили по новым группам, причем так, что группы снова получились равные по численности. Известно, что всего есть 1512 первокурсников и число студентов в группе оказалось меньше 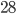 . Сколько стало групп? Ответ: 63
. Сколько стало групп? Ответ: 63 - Автоматы двух типов красили детали, и все детали были покрашены за
 ч. Определите количество автоматов, если каждый из них мог бы покрасить все детали за целое число часов, общая сумма которых (для всех автоматов) равна 55. Ответ: 7
ч. Определите количество автоматов, если каждый из них мог бы покрасить все детали за целое число часов, общая сумма которых (для всех автоматов) равна 55. Ответ: 7 - В двух ящиках находится более
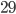 одинаковых деталей. Число деталей в первом ящике, уменьшенное на
одинаковых деталей. Число деталей в первом ящике, уменьшенное на 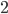 , более чем в три раза превышает число деталей во втором ящике. Утроенное число деталей в первом ящике превышает удвоенное число деталей во втором ящике, но менее, чем на 60. Сколько деталей в каждом ящике? Ответ: в первом 24, во втором 7.
, более чем в три раза превышает число деталей во втором ящике. Утроенное число деталей в первом ящике превышает удвоенное число деталей во втором ящике, но менее, чем на 60. Сколько деталей в каждом ящике? Ответ: в первом 24, во втором 7. - Две бригады однотипных тракторов задействованы на вспашке поля. Время вспашки поля одной первой бригадой отличается от времени вспашки поля одной второй бригадой не более чем на
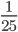 часть времени вспашки поля одним трактором. Если сначала восьмая часть первой бригады вспашет первую половину поля, а затем пятая часть второй бригады вспашет оставшуюся половину поля, то затраченное на вспашку поля время составит
часть времени вспашки поля одним трактором. Если сначала восьмая часть первой бригады вспашет первую половину поля, а затем пятая часть второй бригады вспашет оставшуюся половину поля, то затраченное на вспашку поля время составит 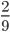 от времени вспашки поля одним трактором. Определите количество тракторов в каждой бригаде. Ответ: в первой 24, во второй 45 тракторов.
от времени вспашки поля одним трактором. Определите количество тракторов в каждой бригаде. Ответ: в первой 24, во второй 45 тракторов. - На складе хранилось более 100 одинаковых коробок с заготовками. Вследствие потребления количество заготовок через некоторое время уменьшилось. Когда в каждой коробке оставалось по 7 заготовок, на склад привезли еще 14 полных коробок, после чего общее количество заготовок оказалось на 3 меньше, чем до потребления. Сколько коробок с заготовками хранилось на складе первоначально? Ответ: 115
- В двух автобусах более 24 человек. Если из второго автобуса выйдут 15 человек, то удвоенное число оставшихся там людей будет меньше числа людей в первом автобусе. Если из первого автобуса выйдут 5 человек, то в 7 раз увеличенное число оставшихся там людей будет меньше числа людей во втором автобусе. Сколько людей в каждом автобусе? Ответ: 7 и 18