Теория чисел
Задачи 141-160

- Найдите минимальное натуральное число, которое при делении на 2, 3, ..., 10 дает в остатке соответственно 1, 2, ... , 9.
- Известно, что
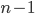 делится на 15, а 1001 делится на
делится на 15, а 1001 делится на 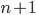 . Найдите
. Найдите 
- В киоске были проданы одинаковые комплекты, состоящие только из синих и красных карандашей, причем в каждом комплекте число синих карандашей более чем на 3 превосходило число красных. Если бы в каждом комплекте число синих карандашей увеличили в 3 раза, а число красных - в 2 раза, то число синих карандашей в одном комплекте превосходило бы число красных не более чем на 16, а общее число всех проданных карандашей равнялось бы 81. Определите, сколько продано комплектов и сколько в каждом комплекте синих и красных карандашей.
- Найдите натуральные решения уравнения
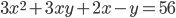
- Найдите натуральные решения уравнения
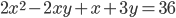
- После деления некоторого двузначного числа на сумму его цифр в частном получается 7, а в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найдите это двузначное число.
- На факультет подано от школьников на 600 заявлений больше, чем от производственников. Девушек среди школьников в 5 раз больше, чем девушек среди производственников, а юношей среди школьников больше, чем юношей среди производственников, в
 раз, причем
раз, причем 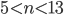 (
( - целое число). Определите общее количество заявлений, если юношей среди производственников на 20 больше, чем девушек среди производственников.
- целое число). Определите общее количество заявлений, если юношей среди производственников на 20 больше, чем девушек среди производственников. - Число двухкомнатных квартир в доме в 4 раза больше числа однокомнатных, а число трехкомнатных квартир кратно числу однокомнатных. Если число трехкомнатных квартир увеличить в 5 раз, то их станет на 22 больше, чем двухкомнатных. Сколько всего квартир в доме, если известно, что их не меньше 100?
- Линию, связывающую города А и В, обслуживают самолеты трех типов. Каждый самолет первого, второго и третьего типов может принять на борт соответственно 230, 110 и 40 пассажиров, а также 27, 12 и 5 контейнеров. Все самолеты линии могут принять на борт одновременно 760 пассажиров и 88 контейнеров. Найдите число действующих на линии самолет каждого типа, зная, что их общее число не превосходит 8.
- Натуральные числа
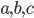 , взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2240 и 4312 делятся на
, взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2240 и 4312 делятся на  и
и  соответственно. Найдите
соответственно. Найдите 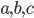 , если известно, что при указанных условиях сумма
, если известно, что при указанных условиях сумма 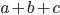 максимальна.
максимальна. - При перемножении двух натуральных чисел, разность которых равна 10, была допущена ошибка: цифра сотен в произведении увеличена на 2. При делении полученного (неверного) произведения на меньший множитель получены частное 50 и остаток 25. Найдите множители.
- Мастер делает за 1 час целое число деталей, большее 5, а ученик - на 2 детали меньше. Один мастер выполняет заказ за целое число часов, а два ученика вместе - на 1 час быстрее. Из какого количества деталей состоит заказ?
- Совокупность А состоит из различных натуральных чисел. Количество чисел в А не меньше восьми. Наименьшее общее кратное всех чисел из А равно 462. Для любых двух чисел из А их наименьшее общее кратное меньше 250. Произведение всех чисел из А, умноженное на 9, является кубом целого числа. Найдите числа, из которых состоит А.
- Сколько существует четырехзначных чисел, которые в 600 раз больше суммы своих цифр?
- Какое трехзначное число равно кубу цифр его единиц, а также квадрату числа, составленного из его второй и третьей цифр?
- Найдите двузначное число, если известно, что при делении этого числа на сумму его цифр в частном получается 4 и в остатке 3. Если же из искомого числа вычесть удвоенную сумму его цифр, то получится 25.
- Партию деталей решили поровну разложить по ящикам. Сначала в каждый ящик положили по 12 деталей, но при этом осталась одна деталь. Тогда из одного ящика вынули все детали, и в оставшиеся ящики удалось разложить детали поровну. Сколько деталей было в партии, если в каждый ящик помещается не более 20 деталей?
- Разность цифр двузначного натурального числа А равна 4, а сумма квадратов цифр А больше произведения его цифр на 37. Найдите А.
- Докажите, что если
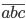 делится на 37, то и
делится на 37, то и 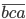 , и
, и 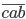 тоже делятся на 37.
тоже делятся на 37. - Докажите, что числа вида
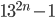 делятся на 168.
делятся на 168.