Теория чисел
Задачи 201-220

- Последовательность
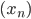 задана формулами
задана формулами 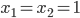 и
и 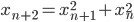 , если
, если 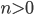 . Делится ли
. Делится ли 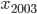 на 7?
на 7? - Последовательность
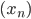 задана формулами
задана формулами 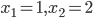 и
и 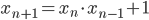 , если
, если 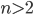 . Докажите, что ни одно из чисел этой последовательности не делится на 4.
. Докажите, что ни одно из чисел этой последовательности не делится на 4. - Докажите, что для любого целого
 либо
либо 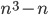 , либо
, либо 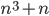 делится на 10
делится на 10 - Докажите, что если
 нечетно, то
нечетно, то 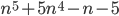 делится на 80.
делится на 80. - Докажите, что
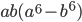 делится на 42 при любых целых
делится на 42 при любых целых  и
и 
- Докажите, что среди любых
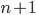 натуральных чисел найдутся два, разность которых делится на
натуральных чисел найдутся два, разность которых делится на 
- Докажите, что для любого целого числа
 в последовательности
в последовательности 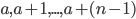 ровно одно из чисел делится на
ровно одно из чисел делится на 
- Докажите, что для любого нечетного
 найдется такое натуральное
найдется такое натуральное  , что
, что 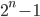 делится на
делится на 
- Докажите, что наименьшее число, взаимно простое с числами 2, 3, ...,
 , просто
, просто - Докажите, что для любого натурального
 найдется такое натуральное
найдется такое натуральное  , что число
, что число 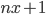 составное
составное - Докажите, что если число, являющееся квадратом некоторого целого числа, делится на простое число
 , то оно должно делиться и на число
, то оно должно делиться и на число 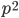
- При каких целых
 число
число 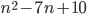 является простым?
является простым? - При каких целых
 число
число 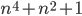 является простым?
является простым? - Про три простых числа известно, что одно из них является разностью кубов двух других. Какие это числа?
- Докажите, что если
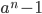 - простое число, то
- простое число, то 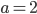 и
и  - простое число
- простое число - Докажите, что если
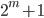 - простое число, то
- простое число, то 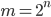 для некоторого целого неотрицательного
для некоторого целого неотрицательного 
- Найдите все простые числа
 такие, что числа
такие, что числа 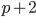 и
и 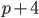 также простые
также простые - Какие остатки при делении на 6 может иметь простое число, большее 3?
- Докажите, что если
 и
и 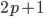 - простые число, большие 6, то число
- простые число, большие 6, то число 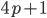 составное
составное - Известно, что числа
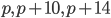 - простые. Найдите
- простые. Найдите  .
.