Теория чисел
Задачи 221-240

- Известно, что числа
 и
и 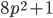 - простые. Найдите
- простые. Найдите 
- Известно, что числа
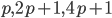 - простые. Найдите
- простые. Найдите 
- Найдите все такие простые числа
 , что число
, что число 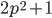 также простое.
также простое. - Докажите, что число
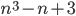 составное для любого натурального
составное для любого натурального 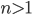
- Найдите все такие простые числа
 , что числа
, что числа 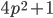 и
и 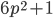 также простые
также простые - Докажите, что остаток от деления простого числа на 30 либо является простым числом, либо равен 1
- Докажите, что если
\((n-1)\)не делится на , то либо
, то либо 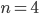 , либо
, либо  - простое число
- простое число - Пусть
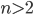 . Докажите, что произведение всех простых чисел, не превосходящих
. Докажите, что произведение всех простых чисел, не превосходящих  , больше
, больше 
- Докажите, что если
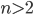 , то между числами
, то между числами  и
и \(n\)есть простое число. - Докажите, что если число
 - составное, то число
- составное, то число 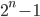 тоже составное
тоже составное - Докажите, что квадрат простого числа, большего трех, дает остаток 1 при делении на 12
- Докажите, что для любого натурального числа
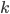 в натуральном ряду можно найти
в натуральном ряду можно найти 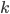 идущих подряд составных чисел
идущих подряд составных чисел - Найдите простое число
 , если число
, если число 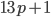 является кубом некоторого натурального числа.
является кубом некоторого натурального числа. - Докажите, что сумма
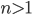 последовательных нечетных чисел является составным числом
последовательных нечетных чисел является составным числом - Докажите, что если
 - простое число, то число
- простое число, то число 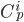 при
при 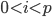 делится на
делится на  . Верно ли это утверждение, если число
. Верно ли это утверждение, если число  не является простым?
не является простым? - Докажите, что число вида
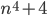 ,
, 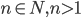 всегда составное.
всегда составное. - Обозначим через
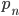 n-ое по порядку простое число. Докажите, что
n-ое по порядку простое число. Докажите, что 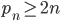
- Пусть
 - простое число. Докажите, что единственным решением в целых числах уравнения
- простое число. Докажите, что единственным решением в целых числах уравнения 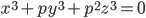 является
является 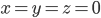
- Докажите, что существует бесконечно много простых чисел, дающих при делении на 3 остаток 2.
- Докажите, что простых чисел вида
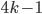 бесконечно много.
бесконечно много.