Теория чисел
Задачи 241-260

- Из чисел от 1 до 1000! вычеркнуты все числа, делящиеся на 2, 3, 5 и 7. Какая часть первоначально взятых чисел осталась невычеркнутой?
- Числа b и c взаимно просты. Сколько имеется чисел от 1 до a, делящихся хотя бы на одно из чисел b и c?
- Докажите, что число
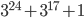 является составным.
является составным. - Найдите все упорядоченные тройки простых чисел
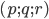 , удовлетворяющие равенству
, удовлетворяющие равенству 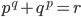
- Докажите, что a не может быть четвертой степенью натурального числа, если a-5 делится на 9.
- Докажите, что число вида 8n+7 не может быть суммой квадратов трех целых чисел.
- Докажите, что сумма четных степеней трех последовательных четных чисел не может равняться четной степени целого числа.
- Решите сравнения: а)
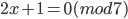 ; б)
; б) 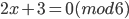 ; в)
; в) 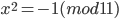 ; г)
; г) 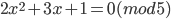
- Решите сравнения: а)
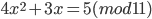 ; б)
; б) 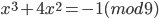
- Решите систему сравнений
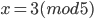 и
и 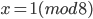
- Докажите, что числа вида
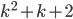 не могут делиться на числа вида
не могут делиться на числа вида 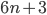
- Докажите, что числа вида
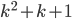 не могут делиться на 5, на 11, на 17.
не могут делиться на 5, на 11, на 17. - Докажите, что ни при каком натуральном
 число
число 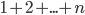 не может заканчиваться ни одной из цифр 2, 4, 7, 9.
не может заканчиваться ни одной из цифр 2, 4, 7, 9. - Найдите остаток от деления числа
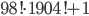 на 2003
на 2003 - Докажите, что число
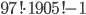 делится на 2003
делится на 2003 - На доске написано число
 . За каждый ход его можно заменить либо на число
. За каждый ход его можно заменить либо на число 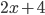 , либо на число
, либо на число 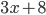 , либо на число
, либо на число 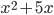 . Можно ли за несколько таких ходов из числа 3 получить число 2002?
. Можно ли за несколько таких ходов из числа 3 получить число 2002? - Докажите, что НОД(a,b)=НОД(a,a+b)=НОД(a,a-b)
- Докажите, что если целые числа a и b взаимно просты, то их сумма и произведение также являются взаимно простыми числами.
- Докажите, что если числа a и b являются взаимно простыми, то НОД(a+b,a-b) равен либо 1, либо 2. Приведите пример таких взаимно простых чисел a и b, что НОД(a+b, a-b)=2
- Докажите, что если числа a и b являются взаимно простыми, то НОД(
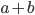 ,
,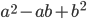 ) равен либо 1, либо 3. Приведите пример таких взаимно простых чисел a и b, что НОД(
) равен либо 1, либо 3. Приведите пример таких взаимно простых чисел a и b, что НОД(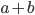 ,
,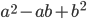 )=3
)=3