Теория чисел
Задачи 321-340

- Докажите, что уравнение не имеет решений в целых числах: а)
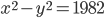 ; б)
; б) 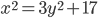 ; в)
; в) 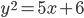 ; г)
; г) 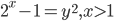 ; д)
; д) 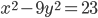 ; е)
; е) 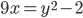 ; ж)
; ж) 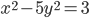
- Решите в натуральных числах уравнение
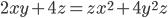
- Решите в натуральных числах уравнение
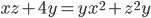
- Решите в натуральных числах уравнение
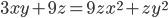
- Решите в натуральных числах уравнение
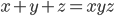
- Решите в натуральных числах уравнение
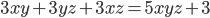
- Решите в целых числах уравнение
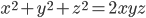
- Решите в целых числах уравнение
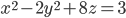
- Сколько различных целочисленных пар удовлетворяют уравнению
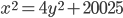 ?
? - Найдите натуральное число
 , если: а)
, если: а)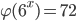 ; б)
; б) 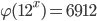 ; в)
; в) 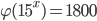
- Докажите, что для любого целого числа
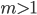 сумма всех натуральных чисел, не превосходящих числа
сумма всех натуральных чисел, не превосходящих числа  и взаимно простых с
и взаимно простых с  , равна
, равна 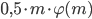
- Найдите все натуральные числа
 , для которых имеет место равенство
, для которых имеет место равенство 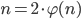
- Найдите остаток от деления
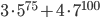 на 132
на 132 - Докажите, что если
 и
и 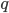 произвольные простые числа, то для любого целого числа
произвольные простые числа, то для любого целого числа  имеет место сравнение
имеет место сравнение 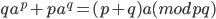
- Решите уравнение
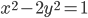 в рациональных числах
в рациональных числах - Решите уравнение
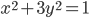 в рациональных числах
в рациональных числах - Мастер делает в час целое число деталей, большее, чем 15, а ученик - на 5 деталей меньше. Один мастер выполняет заказ за целое число часов, а два ученика вместе - на 1 час быстрее. Из какого количества деталей состоит заказ?
- При каких
 система неравенств
система неравенств 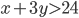 ,
, 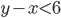 и
и 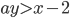 имеет единственное решение в целых числах?
имеет единственное решение в целых числах? - Найдите сумму всех семизначных четных чисел, делящихся на 3 и записываемых только цифрами 0 и 1.
- Стороны прямоугольника выражены целыми числами. Каковы длины сторон прямоугольника, если его периметр численно равен площади?