Решебник домашнего задания урока 13 В.В. Ткачук "Математика - абитуриенту"
Задача 21

Рассмотрим решение задачи 21 домашнего задания 13 на тему: "Текстовые задачи. Движение". Условие задачи:
Из пункта А в пункт В выезжает автомобиль и одновременно из В в А с меньшей скоростью выезжает мотоцикл. Через некоторое время они встречаются, и в этот момент из В в А выезжает второй мотоцикл, который встречается с автомобилем в точке, отстоящей от точки встречи автомобиля с первым мотоциклом на расстоянии, равном 2/9 пути от А до В. Если бы скорость автомобиля была на 20 км/ч меньше, то расстояние между точками встречи равнялось бы 72 км и первая встреча произошла бы через 3 часа после выезда автомобиля из пункта А. Найти длину пути от А до В (скорости мотоциклов одинаковы).
Ответ должен быть 300 км, что совпадет с нашим ответом.
Пусть на отрезке AB точка C - место встречи автомобиля с первым мотоциклом, точка D - место встречи со вторым мотоциклом. Причем точка D находится между точками C и B. Если AB = 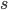 , скорость мотоцикла
, скорость мотоцикла 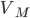 , скорость автомобиля
, скорость автомобиля 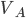 , AC =
, AC =  , то CD =
, то CD = 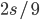 , CB =
, CB =  и DB =
и DB = 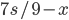 . Так как по условию автомобиль и первый мотоцикл выехали одновременно, то
. Так как по условию автомобиль и первый мотоцикл выехали одновременно, то 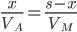 . То есть затраченное время каждым одинаково на путь до встречи. Аналогично для автомобиля и второго мотоцикла с момента первой встречи автомобиля до второй встречи:
. То есть затраченное время каждым одинаково на путь до встречи. Аналогично для автомобиля и второго мотоцикла с момента первой встречи автомобиля до второй встречи: 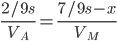 .
.
Из первого уравнения выразим 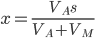 и подставим во второе. После упрощения получаем
и подставим во второе. После упрощения получаем 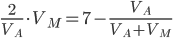 , то есть
, то есть 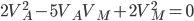 . Разделим левую и правую части уравнения на
. Разделим левую и правую части уравнения на 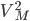 и получим квадратное уравнение относительно
и получим квадратное уравнение относительно 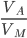 :
: 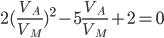 . Находим, что
. Находим, что 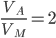 или
или 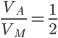 . Так как по условию скорость мотоцикла меньше, то
. Так как по условию скорость мотоцикла меньше, то 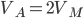 .
.
Далее рассмотрим случай, когда скорость автомобиля на 20 меньше. Точки C и D будут иметь тот же смысл, что и в первом случае. Пусть AC = y, CD = 72, DB = s- y -72, CB = s - y. Тогда можно составить уравнения: 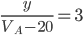 ,
, 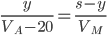 и
и 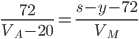 . Из первого и второго уравнений выражаем y и приравниваем:
. Из первого и второго уравнений выражаем y и приравниваем: 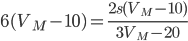 , откуда
, откуда 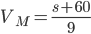 .
.
Далее в третье уравнение подставляем найденные выражения так, чтобы осталась только неизвестная s: 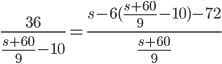 . Получаем
. Получаем 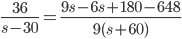 , откуда
, откуда 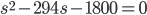 и
и 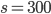 .
.
Список домашний заданий и их решений здесь. Спасибо за внимание.