Решебник домашнего задания урока 1
В.В. Ткачук "Математика - абитуриенту"
Задачи 15-17

Рассмотрим решение задач с номерами 15-17 домашнего задания урока 1 на тему: "Тригонометрические уравнения. Сведение к квадратным уравнениям". Весь список домашних заданий и их решений здесь.
Задача 15. 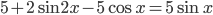 . Применим формулу двойного аргумента
. Применим формулу двойного аргумента 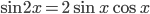 и представим
и представим 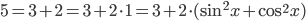 . Тогда уравнение примет вид
. Тогда уравнение примет вид 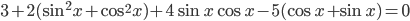
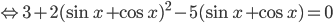
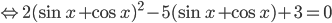 . Далее решаем как квадратное относительно
. Далее решаем как квадратное относительно 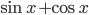 (или можно сделать замену
(или можно сделать замену 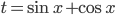 для более наглядного представления). Получаем, что
для более наглядного представления). Получаем, что 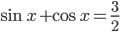 или
или 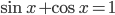 . Так как
. Так как 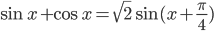 , то уравнения принимают вид
, то уравнения принимают вид 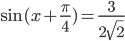 и
и 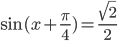 . Первое уравнение коней не имеет, так как
. Первое уравнение коней не имеет, так как 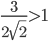 . Для второго уравнения
. Для второго уравнения 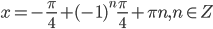 .
.
Задача 16. [2] Необходимо решить уравнение 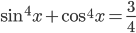 . Применим формулу
. Применим формулу 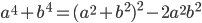 к левой части уравнения. Тогда
к левой части уравнения. Тогда 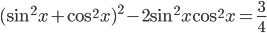 . Так как
. Так как 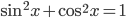 и
и 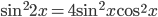 , то уравнение примет вид
, то уравнение примет вид 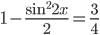
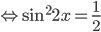
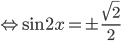 , откуда
, откуда 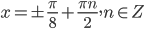 .
.
Задача 17. 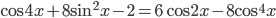 . Применим формулы понижения степени
. Применим формулы понижения степени 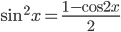 и
и 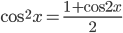 . Получим уравнение
. Получим уравнение 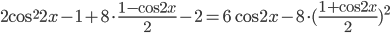
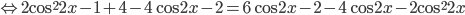
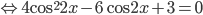 . Пришли к квадратному относительно
. Пришли к квадратному относительно 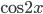 уравнению с отрицательным дискриминантом.
уравнению с отрицательным дискриминантом.