Урок 17. Прогрессии
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Известно, что
 - арифметическая прогрессия и
- арифметическая прогрессия и 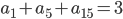 . Найдите
. Найдите 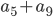 .
. - Известно, что
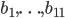 - геометрическая прогрессия и
- геометрическая прогрессия и 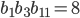 . Найдите
. Найдите 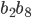 .
. - Найдите трехзначное число, цифры которого образуют (в том порядке, в котором они стоят в числе) возрастающую арифметическую прогрессию и которое делится на 45.
- [2] Найдите все значения
 , при которых уравнение
, при которых уравнение 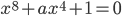 имеет ровно четыре корня и эти корни образуют арифметическую прогрессию.
имеет ровно четыре корня и эти корни образуют арифметическую прогрессию. - Про натуральные числа
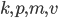 известно следующее:
известно следующее: 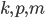 - геометрическая прогрессия,
- геометрическая прогрессия, 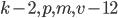 - арифметическая прогрессия и
- арифметическая прогрессия и 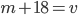 . Найдите
. Найдите  .
. - Найдите сумму чисел, являющихся одновременно членами прогрессии 3, 7, 11, ..., 203 и прогрессии 2, 9, 16, ..., 212.
- Второй член арифметической прогрессии, состоящей из целых чисел, равен 2, а сумма квадратов третьего и четвертого ее членов равна 4. Найдите первый член прогрессии.
- Известно, что
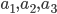 - геометрическая прогрессия, знаменатель которой
- геометрическая прогрессия, знаменатель которой 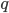 - натуральное число, причем
- натуральное число, причем 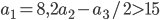 . Найдите
. Найдите 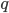 .
. - Пусть
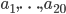 - арифметическая прогрессия,
- арифметическая прогрессия, 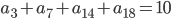 . Найдите
. Найдите 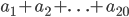 .
. - [3] Могут ли числа
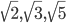 быть членами (не обязательно последовательными) одной арифметической прогрессии?
быть членами (не обязательно последовательными) одной арифметической прогрессии? - Известно, что
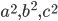 - арифметическая прогрессия. Докажите, что тогда и
- арифметическая прогрессия. Докажите, что тогда и 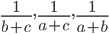 - тоже арифметическая прогрессия.
- тоже арифметическая прогрессия. - [2] Известно, что при любом
 сумма первых
сумма первых  членов некоторой числовой последовательности выражается формулой
членов некоторой числовой последовательности выражается формулой 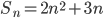 . Найдите десятый член этой последовательности и докажите, что она является арифметической прогрессией.
. Найдите десятый член этой последовательности и докажите, что она является арифметической прогрессией. - [3] Найдите сумму
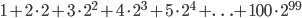 .
. - Известно, что
 - геометрическая прогрессия с положительными членами,
- геометрическая прогрессия с положительными членами, 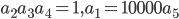 . Найдите все члены этой прогрессии.
. Найдите все члены этой прогрессии. - [2] Известно, что
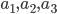 и
и 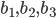 - арифметические прогрессии, причем
- арифметические прогрессии, причем 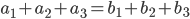 и
и 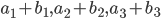 - геометрическая прогрессия. Докажите, что
- геометрическая прогрессия. Докажите, что 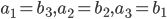 .
.
Ответы к домашнему заданию урока 17 из В.В. Ткачук "Математика - абитуриенту"
- 2
- 4
- 135
- -82/9
- 18
- 749
- 3
- 2
- 50
- не могут
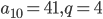
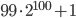
- 100, 10, 1, 1/10, 1/100