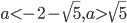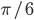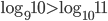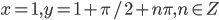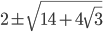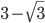Урок 40. Использование различных свойств функции
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
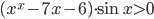
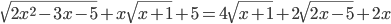
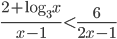
- Найдите все значения параметра
 , при которых неравенство
, при которых неравенство 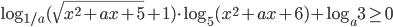 имеет ровно одно решение.
имеет ровно одно решение. 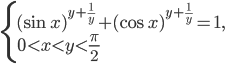
- Найдите все значения параметра
 из интервала (2; 5), при которых уравнение
из интервала (2; 5), при которых уравнение 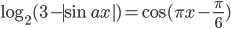 имеет хотя бы одно решение из отрезка [2;3].
имеет хотя бы одно решение из отрезка [2;3]. - Найдите все
 , при которых уравнение
, при которых уравнение 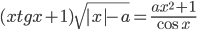 имеет нечетное число корней.
имеет нечетное число корней. - Доказать, что для любых
 и
и 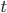 справедливо неравенство
справедливо неравенство 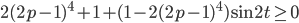 , и найти все пары
, и найти все пары 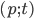 , при которых оно обращается в равенство.
, при которых оно обращается в равенство. - Среди всех решений
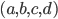 системы
системы 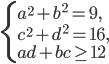 найдите такие, при которых величина
найдите такие, при которых величина 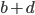 принимает наименьшее значение.
принимает наименьшее значение. - Найдите все
 , при которых функция
, при которых функция 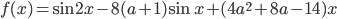 является возрастающей на всей числовой прямой и при этом не имеет критических точек.
является возрастающей на всей числовой прямой и при этом не имеет критических точек. - Найдите все
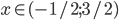 , удовлетворяющие уравнению
, удовлетворяющие уравнению 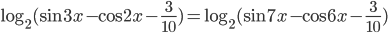 .
. - Что больше,
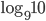 или
или 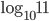 ?
? 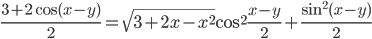
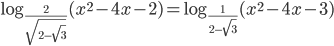
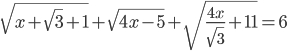
Ответы к домашнему заданию урока 40 из В.В. Ткачук "Математика - абитуриенту"
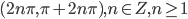
- 6
- (1/2;1)
- 2
- x = t, y = 1, 0<t<1
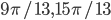
- -1
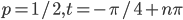
- a=-12/5, b=-9/5, c=-12/5, d=-16/5