Урок 18. Показательные уравнения, неравенства и системы
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
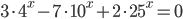
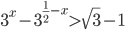
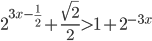
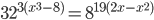
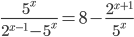
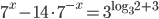
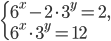
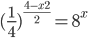
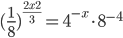
![7^{x-\frac{x^2}{8}}<7^{1-x}\cdot (\sqrt[\displaystyle�8]{7})^{x^2}+6](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a4292cdb764656473df1f9d58483f411.gif)
![5^{2x-\frac{x^2}{3}}<5^{2-2x}\cdot (\sqrt[\displaystyle�3]{5})^{x^2}+24](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_5f8baaf403c1b481281f884197208ffc.gif)
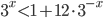
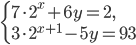
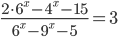
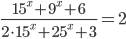
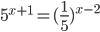
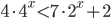
- [2]
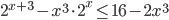
- [2]
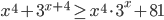
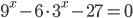
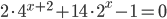
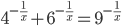
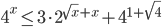
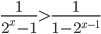
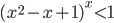
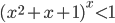
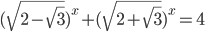
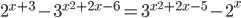
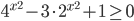
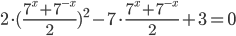
Ответы к домашнему заданию урока 18 из В.В. Ткачук "Математика - абитуриенту"
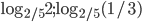
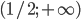
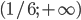
- 2; -5; -4/5
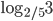
- 1
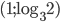
- 4; -1
- 3; -2
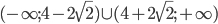
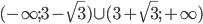
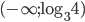
- (3;-9)
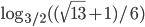
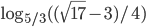
- 1/2
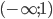
![(-\infty; 1]\cup [2; +\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_6b3b24a933bfa21d898afa22f93f2139.gif)
![(-\infty; -3]\cup [0;3]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_6098551361570cb9be27a16482c863c0.gif)
- 2
- -4
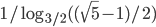
- [0;4]
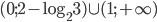
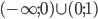
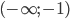
- 2; -2
- 2;
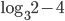
![(-\infty; -\sqrt{\log_2(3+\sqrt{5})-1}]\cup[\sqrt{\log_2(3+\sqrt{5})-1};+\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_f8a39346823a972364bc80eeedbb1cc6.gif)