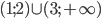Урок 21. Задачи, содержащие логарифмы, модули, радикалы и т.п.
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
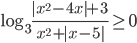
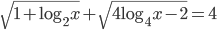
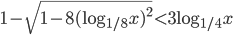
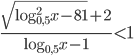
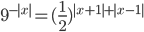
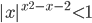
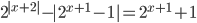
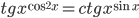
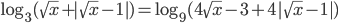
- [2]
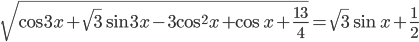
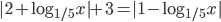
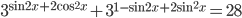
- [2]
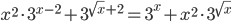
- [2]
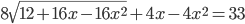
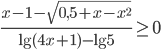
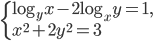
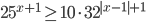
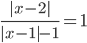
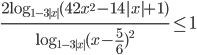
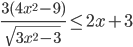
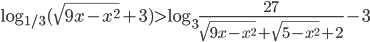
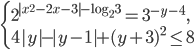
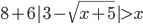
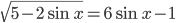
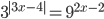
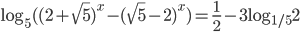
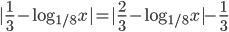
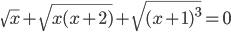
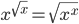
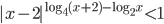
Ответы к домашнему заданию урока 21 из В.В. Ткачук "Математика - абитуриенту"
![(-\infty; -2/3]\cup [1/2; 2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_592e40aceda3f6149cc03c2dc45f9d9b.gif)
- 8
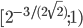
![(2^{-15}; 2^{-9}]\cup [512; +\infty)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_1d304483df9a1d8cfc252b00cb1efa7e.gif)
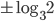
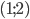
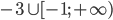
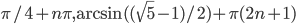
- [0;1]U{4}
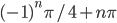
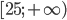
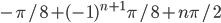
- 3; 4
- 1/2
![[(3+\sqrt{5})/4; (1+\sqrt{3})/2]\cup (-1/4; 1)](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_90f6c59aaa3171f11cd3f28b6edbc79d.gif)
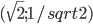
![[\frac{11-\log_25}{5+2\log_25}; \frac{\log_25-1}{5-\log_25}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_1815c7d3fc6c3e9f13d0f83d1676621f.gif)
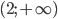
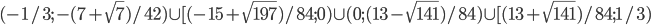
- [-3/2; -1)U(1;2]
- [0;2)
- (3;-3), (-1;-3)
- [-5; 20)
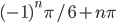
- 8/7
- 2
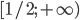
- нет решений
- 1; 4