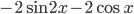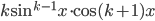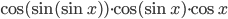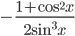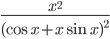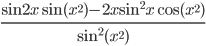Урок 22. Вычисление производной функции
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
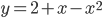 . Найдите
. Найдите 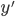 .
.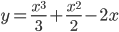 . Найдите
. Найдите 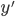 .
.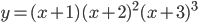 . Найдите
. Найдите 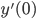 .
.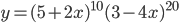 . Найдите
. Найдите 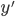 .
.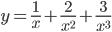 . Найдите
. Найдите 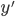 .
.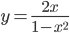 . Найдите
. Найдите 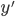 .
.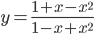 . Найдите
. Найдите 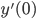 .
.![y=\sqrt[3]{\frac{1+x^3}{1-x^3}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7a5e49e18aa4b7a251b51b48d8e5ebd7.gif) . Найдите
. Найдите 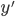 .
.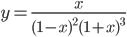 . Найдите
. Найдите 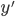 .
.![y=x+\sqrt{x}+\sqrt[3]{x}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_0fa6de767d0ebc5c5904d000b73c3186.gif) . Найдите
. Найдите 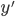 .
.![y=\frac{1}{x}+\frac{1}{\sqrt{x}}+\frac{1}{\sqrt[3]{x}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_bdd93fcae72f62b57114eab942e29371.gif) . Найдите
. Найдите 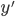 .
.![y=\sqrt[3]{x^2}-\frac{2}{\sqrt{x}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_229b9a9b8d6015b3ea920cbbb92d82c5.gif) . Найдите
. Найдите 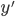 .
.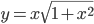 . Найдите
. Найдите 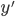 .
.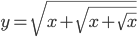 . Найдите
. Найдите 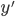 .
.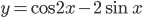 . Найдите
. Найдите 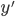 .
.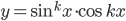 . Найдите
. Найдите 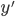 .
.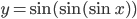 . Найдите
. Найдите 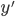 .
.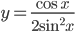 . Найдите
. Найдите 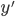 .
.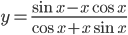 . Найдите
. Найдите 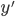 .
.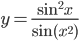 . Найдите
. Найдите 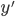 .
.
Ответы к домашнему заданию урока 22 из В.В. Ткачук "Математика - абитуриенту"
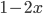
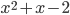
- 324
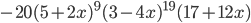
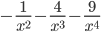
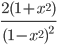
- 2
![\frac{2x^2}{\sqrt[3]{(1+x^3)^2(1-x^3)^4}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_0c118d331e93c257342caf30c824a6ae.gif)
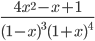
![10+\frac{1}{2\sqrt{x}}+\frac{1}{3\sqrt[3]{x^2}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_889b360ce73a18e9a97fdf79869ce63f.gif)
![-\frac{1}{x^2}-\frac{1}{2x\sqrt{x}}-\frac{1}{3x\sqrt[3]{x}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_f8df9f0fe20541317b52a37bdf5794ec.gif)
![\frac{2}{3\sqrt[3]{x}}+\frac{1}{x\sqrt{x}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b4db8e9f58e0890ef09dd62f332134ec.gif)
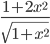
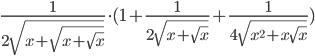
-