В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 28

Урок 28. Подобие

Домашнее задание из В.В. Ткачук “Математика – абитуриенту”

  1. Точки A, B, C, D лежат на одной прямой, причем С находится между А и D, а точка B – между A и C. Известное, что AB:BC = k, BC:CD = p. Найдите AC:BD.
  2. Точки A, B, C, D лежат на одной прямой, причем С находится между А и D, а точка B – между A и C. Известное, что AD:CD = k, AC:BC = p. Найдите AB:BD.
  3. Точки A, B, C, D лежат на одной прямой, причем С находится между А и D, а точка B – между A и C. Известное, что AC:BD = k, AD:BC = p. Найдите AB:CD.
  4. Дан угол с вершиной О. На одном из его лучей расположены точки A, B, C таким образом, что B лежит между A и O, а С – между B и O. Через каждую из этих точек проведены параллельные прямые, пересекающие другую сторону угла соответственно в точках A1, B1 и C1. Известно, что A1C1:B1C1=p, BC:BO=q. Найдите AA1:CC1.
  5. В равносторонний треугольник со стороной 1 вписан квадрат так, что одна из сторон квадрата лежит на стороне треугольника, а на каждой из остальных сторон лежит по одной вершине квадрата. Найдите сторону квадрата.
  6. В трапеции ABCD основание  BC равно 1 и AC:OC=5:2, где О – точка пересечения диагоналей трапеции. Найдите длину основания AD.
  7. В треугольнике ABC угол С прямой, AC = b, BC = a. Найдите AH:HB, где CH – высота, опущенная из вершины С.
  8. Две окружности радиусов R и r (R>r) касаются внешним образом. Пусть M – точка пересечения линии центров с общей касательной названных окружностей, а К – точка касания большей окружности с общей касательной. Найдите длину отрезка MK.
  9. Окружность, вписанная в треугольник ABC, касается стороны BC в точке L. Точка P лежит на стороне AB, а точка Q – на стороне  BC так, что PQ касается окружности и PQ параллельно AC. Известно, что BL = 3 и AP:P=7:5. Найдите периметр треугольника ABC.
  10. В треугольнике ABC имеем AB = 6 и AC = 5. Точка A1 лежит на стороне BC таким образом, что AA1 есть биссектриса угла А. Точка C1 лежит на стороне AB таким образом, что A1C1 параллельно AC. Найти  A1C1.
  11. В треугольнике ABC сторона AB равна 7 и угол BAC равен 30о. На стороне AB лежит точка D такая, что AD:DB=5:2 и углы BCD и BAC равны. Найдите tg C.
  12. В выпуклом четырехугольнике ABCD углы ABD и ACD равны, диагонали AC и BD пересекаются в точке О. Известно, что AB = 2, CD = 3, BD = 4 и BO:OD=1:3. Найдите длину диагонали AC.
  13. В трапеции ABCD с основаниями AD и BC имеем AD = 3, BC = 1. Точка P лежит на стороне AB, а точка Q – на стороне CD, причем отрезок PQ параллелен основаниям и проходит через точку пересечения диагоналей трапеции. Найдите длину отрезка PQ.
  14. В трапеции ABCD основание AD равно 2, а основание BC равно 1. Точка P лежит на стороне AB, а точка Q – на стороне CD, причем отрезок PQ параллелен основаниям и AP:PB=3:2. Найдите длину отрезка PQ.
  15. В выпуклом четырехугольнике ABCD углы ABD и ACD прямые, диагонали AC и BD пересекаются в точке О, причем AC – биссектриса угла BAD. Найдите длину отрезка AO, если известно, что AC = 5 и CD = 3.
  16. Точка D лежит на стороне AC треугольника ABC, причем AD = 3, BC = 2, сумма углов ABC и ADB равна 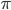$$\pi$$ и косинус угла BDC равен 13/20. Найдите периметр треугольника ABC.
  17. Точка К лежит на стороне АВ, а точка М – на стороне АС треугольника АВС, причем АК:КВ=3:2, АМ:МС=4:5. Прямая, проходящая через точку К параллельно ВС, пересекает отрезок ВМ в точке Р. Найдите отношение ВР:РМ.
  18. Точка К лежит на стороне АВ, а точка М – на стороне АС треугольника АВС, причем АК:КВ=3:2, АМ:МС=4:5. Отрезки КС и ВМ пересекаются в точке О. Найдите отношение ВО:ОМ.
  19. Точка D лежит на стороне АС, а точка Е – на стороне ВС треугольника АВС, причем DE параллельно AB, BC = CD, AB = 8, DE = 3, угол ACB 60о. Найдите длину стороны BC.
  20. На стороне AC треугольника ABC взята точка E. Через точку Е проведена прямая DE параллельно стороне BC и прямая EF параллельно стороне AB (точка D лежит на стороне АВ, а точка F – на стороне BC). Площадь треугольника ADE равна 9, а площадь треугольника EFC равна 4. Найдите площадь параллелограмма BDEF.

Ответы к домашнему заданию урока 28 из В.В. Ткачук “Математика – абитуриенту”

  1. (k+1)p/(p+1)
  2. (k-1)(p-1)/(k+p-1)
  3. (kp-1)/(p-k)
  4. (pq-q+1)/(1-q)
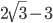
  5. $$2\sqrt{3}-3$$
  6. 3/2
  7. (b/a)2
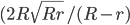
  8. $$(2R\sqrt{Rr}/(R-r)$$
  9. 72/5
  10. 30/11
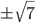
  11. $$\pm\sqrt{7}$$
  12. 7/2
  13. 3/2
  14. 7/5
  15. 16/5
  16. 11
  17. 18:7
  18. 6:5
  19. 24/7
  20. 12


Смотрите:

  1. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 4 Часть 2
  2. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 40
  3. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 30
  4. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 6