Урок 41. Удачная подстановка или группировка
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
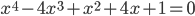
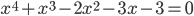
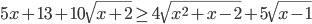
- Решите в целых числах уравнение
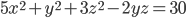 .
. - Найдите наименьшее
 , для которого существуют
, для которого существуют 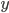 и
и 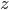 такие, что
такие, что 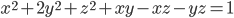 .
. - Пусть
 и
и  - натуральные числа,
- натуральные числа, 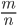 - правильная несократимая дробь. Известно, что дробь
- правильная несократимая дробь. Известно, что дробь 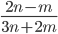 сократима на натуральное
сократима на натуральное 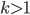 . Найдите все возможные k.
. Найдите все возможные k. 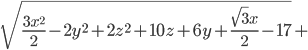
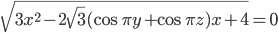
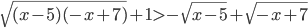
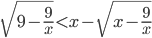
- Решите в целых числах уравнение
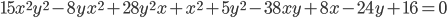 .
. 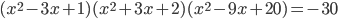
- Для каждого
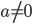 решите уравнение
решите уравнение 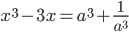 .
. 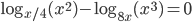
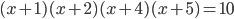
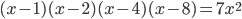
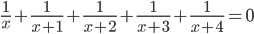
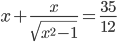
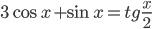
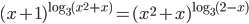
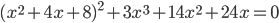
Ответы к домашнему заданию урока 41 из В.В. Ткачук "Математика - абитуриенту"
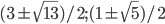
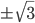
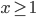
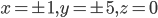
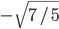
- k = 7
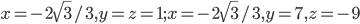
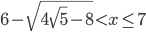
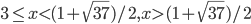
- (-2; -2), (-4; 0), (0; 4)
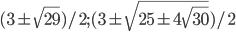
- если а = 1, то х = -1 или х = 2; если a = -1, то х = -2 или х = 1; при остальных a значение x = a+1/a.
- 1; 4096
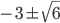
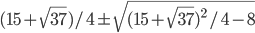
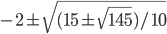
- 5/3; 5/4
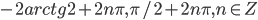
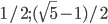
- -4; -2