Урок 35. Уравнения и неравенства с параметрами
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- При каких
 сумма квадратов корней уравнения
сумма квадратов корней уравнения 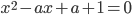 больше 1?
больше 1? - При каких
 сумма кубов уравнения
сумма кубов уравнения 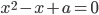 меньше или равна 1?
меньше или равна 1? - При каких
 сумма четвертых степеней корней уравнения
сумма четвертых степеней корней уравнения 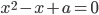 больше или равна 1?
больше или равна 1? - Дано уравнение
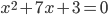 . Пусть
. Пусть 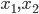 - его корни. Составьте квадратное уравнение с корнями
- его корни. Составьте квадратное уравнение с корнями 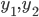 , где
, где 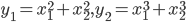 .
. - Дано уравнение
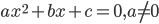 с корнями
с корнями 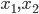 . Составьте квадратное уравнение с корнями
. Составьте квадратное уравнение с корнями 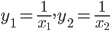 .
. - При каких
 сумма квадратов корней уравнения
сумма квадратов корней уравнения 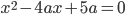 равна 6?
равна 6? - Для всех
 решите неравенство
решите неравенство 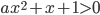 .
. - Для всех
 решите неравенство
решите неравенство 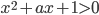 .
. - Для всех
 решите неравенство
решите неравенство 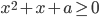 .
. - Для всех
 решите неравенство
решите неравенство 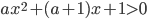 .
. - При каких
 уравнение
уравнение 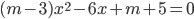 имеет корни? Исследовать их знаки при различных
имеет корни? Исследовать их знаки при различных  .
. - При каких
 уравнение
уравнение 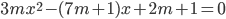 имеет корни? Исследовать их знаки при различных m.
имеет корни? Исследовать их знаки при различных m. - При каких
 сумма квадратов корней уравнения
сумма квадратов корней уравнения 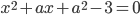 минимальна? Максимальна?
минимальна? Максимальна? - Найдите все
 , при которых уравнения
, при которых уравнения 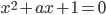 и
и 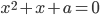 имеют хотя бы один общий корень.
имеют хотя бы один общий корень. - Дано неравенство
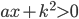 . При каких значениях
. При каких значениях  оно выполнено при всех
оно выполнено при всех  и
и 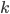 ?
? - Дано неравенство
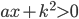 . При каких значениях
. При каких значениях  найдутся такие
найдутся такие  и
и 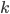 , что оно выполняется?
, что оно выполняется? - Дано неравенство
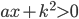 . При каких значениях
. При каких значениях  найдется такое
найдется такое  , что оно выполняется при всех
, что оно выполняется при всех 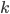 ?
? - Дано неравенство
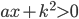 . При каких значениях
. При каких значениях  найдется такое
найдется такое 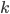 , что оно выполняется при всех
, что оно выполняется при всех  ?
? - Дано неравенство
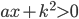 . При каких значениях
. При каких значениях 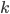 оно выполнено при всех
оно выполнено при всех  и
и  ?
? - Дано неравенство
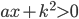 . При каких значениях
. При каких значениях 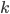 найдется такое
найдется такое  , что оно выполнено при всех
, что оно выполнено при всех  ?
?
Ответы к домашнему заданию урока 35 из В.В. Ткачук "Математика - абитуриенту"
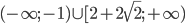
- [0; 1/4]
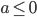
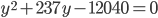
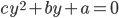
- -3/8
- если а < 0, то
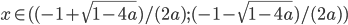 ; если а = 0, то x > -1; если
; если а = 0, то x > -1; если ![a\in (0; 1/4]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_f4d4bbb35d5b6733713507728021fcc5.gif) , то
, то 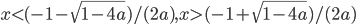 ; если a>1/4, то x любое.
; если a>1/4, то x любое. - если |a|<2, то х любое; если
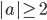 , то
, то 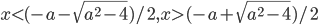
- если а > 1/4, то х любое; если
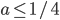 , то
, то 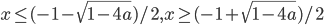
- если а < 0, то -1<x<-1/a; если а = 0, то x > - 1; если
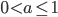 , то x<-1/a, x>-1; если а>1, то x <-1, x>-1/a.
, то x<-1/a, x>-1; если а>1, то x <-1, x>-1/a. - при
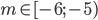 оба корня отрицательны; при m = -5 один из корней равен 0, а второй отрицателен; при -5<m<3 корни имеют различные знаки; при m=3 есть один положительный корень; при
оба корня отрицательны; при m = -5 один из корней равен 0, а второй отрицателен; при -5<m<3 корни имеют различные знаки; при m=3 есть один положительный корень; при 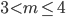 оба корня положительны. При остальных m решений нет.
оба корня положительны. При остальных m решений нет. - при m<-1/2, m>0 оба корня положительны; при m = -1/2 один из корней равен нулю, а другой отрицателен; при m = 0 уравнение имеет один положительный корень; при -1/2<m<0 корни имеют разные знаки
- максимальна при a = 0; минимальна при

- -2
- ни при каких
- при любых а
- при
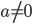
- а = 0
- ни при каких
- при
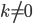
Добрый день!
Подскажите, пожалуйста, способ решения задания номер 3. Откуда выразить сумма четвёртых степеней?
здравствуйте. решение задачи здесь http://www.itmathrepetitor.ru/tkachuk-trigonometricheskie-uravneni-3/